Fatigue cracks are generally the result of periodic plastic deformation in local areas. Fatigue is defined as “failure under repeated load or other types of load conditions, and this load level is not sufficient to cause failure when applied only once.” This plastic deformation occurs not because of the theoretical stress on the ideal component, but because the component surface can not be actually detected.
August Wöhler is the pioneer of fatigue research and puts forward an empirical method. Between 1852 and 1870, w ö hler studied the progressive failure of railway axles. He built the test-bed shown in Figure 1. This test-bed enables two railway axles to be rotated and bent at the same time. W ö hler plotted the relationship between the nominal stress and the number of cycles leading to failure, which is later known as the SN diagram. Each curve is still called a w ö hler line. Sn method is still the most widely used method today. A typical example of this curve is shown in Figure 1.
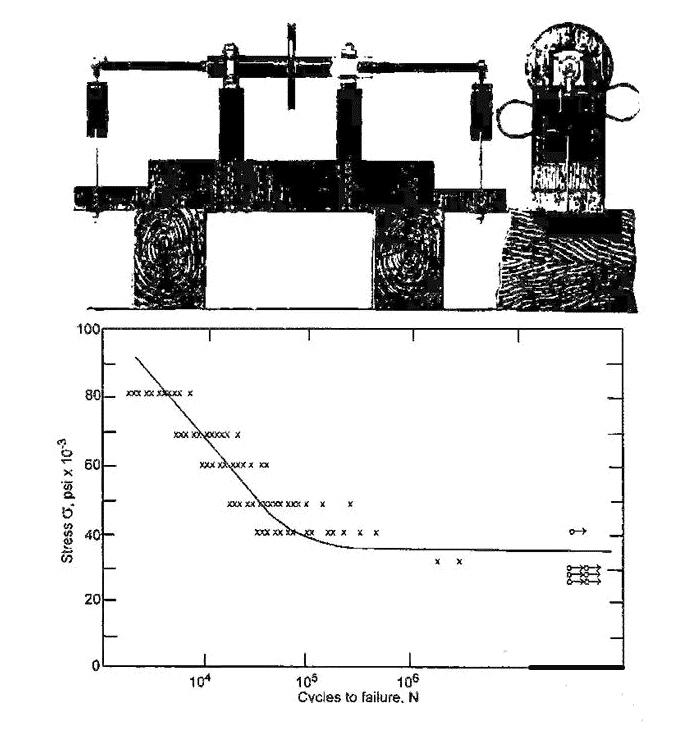
Several effects can be observed through the w ö hler line. First, we note that the SN curve below the transition point (about 1000 cycles) is invalid because the nominal stress here is elastoplastic. We will show later that fatigue is caused by the release of plastic shear strain energy. Therefore, there is no linear relationship between stress and strain before fracture, and it cannot be used. Between the transition point and the fatigue limit (about 107 cycles), the Sn based analysis is valid. Above the fatigue limit, the slope of the curve decreases sharply, so this region is often referred to as the “infinite life” region. But this is not the case. For example, aluminum alloy will not have infinite life, and even steel will not have infinite life under variable amplitude load.
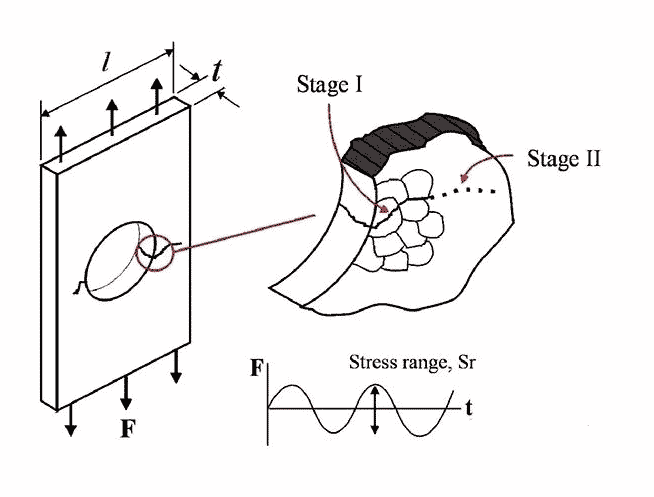
With the emergence of modern amplification technology, people can study fatigue cracks in more detail. We now know that the emergence and propagation of fatigue cracks can be divided into two stages. In the initial stage, the crack propagates at an angle of about 45 degrees relative to the applied load (along the maximum shear stress line). After crossing two or three grain boundaries, its direction changes and extends along the direction of about 90 degrees relative to the applied load. These two stages are called stage I crack and stage II crack, as shown in Figure 2.
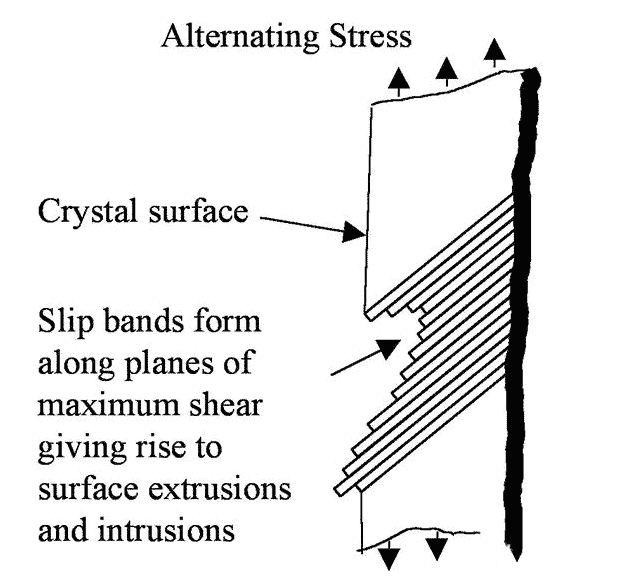
If we observe a stage I crack at high magnification, we can see that the alternating stress will lead to the formation of a continuous slip band along the maximum shear plane. These slip bands slide back and forth, much like a deck of cards, resulting in uneven surfaces. The concave surface finally forms a “budding” crack, as shown in Figure 3. In phase I, the crack will expand in this mode until it meets the grain boundary and will stop temporarily. When enough energy is applied to the adjacent crystals, then the process will continue.
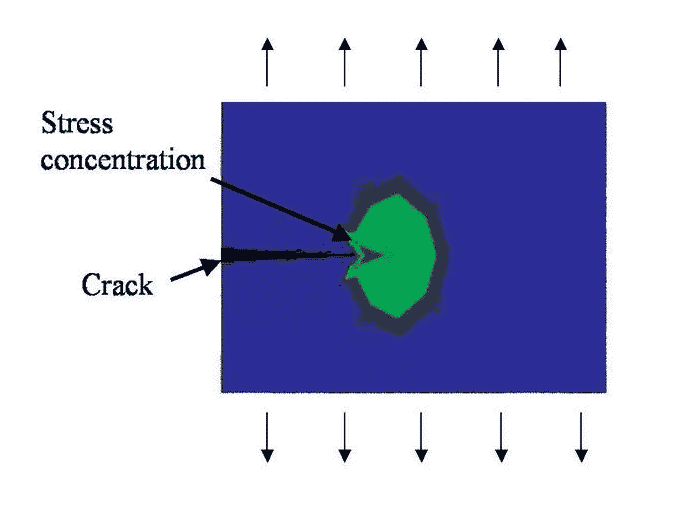
After crossing two or three grain boundaries, the direction of crack propagation now enters phase II mode. At this stage, the physical properties of crack propagation have changed. The crack itself constitutes a macro obstacle to the stress flow, causing high plastic stress concentration at the crack tip. As shown in Figure 4. It should be noted that not all stage I cracks will develop to stage II.
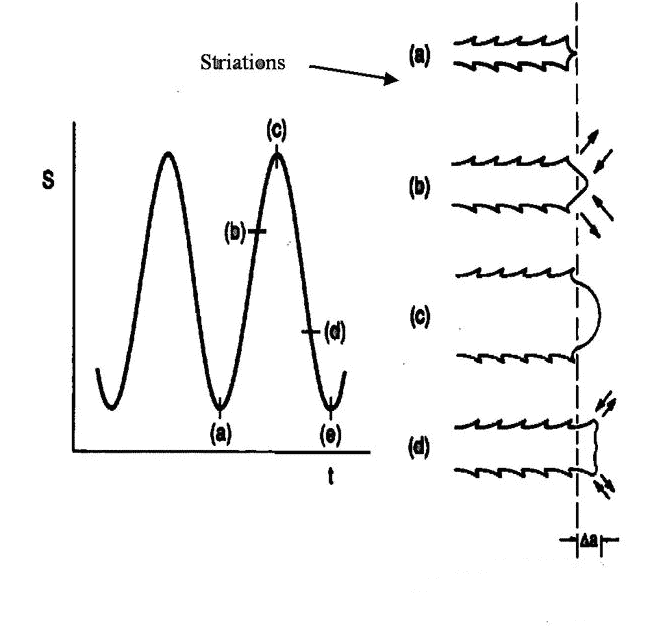
In order to understand the propagation mechanism of stage II, we need to consider the situation of crack tip cross-section during the stress cycle. As shown in Figure 5. The fatigue cycle begins when the nominal stress is at point “a”. As the stress intensity increases and passes through point “B”, we notice that the crack tip opens, resulting in local plastic shear deformation, and the crack extends to point “C” in the original metal. When the tensile stress decreases through the “d” point, we observe that the crack tip closes, but the permanent plastic deformation leaves a unique serration, the so-called “cut line”. When the whole cycle ends at the “e” point, we observe that the crack has now increased the “Da” length and formed additional section lines. It is now understood that the range of crack growth is proportional to the range of applied elastic-plastic crack tip strain. A larger cycle range can form a larger Da.
Factors affecting fatigue crack growth rate
The influence of the following parameters on the fatigue crack growth rate is studied and explained conceptually:
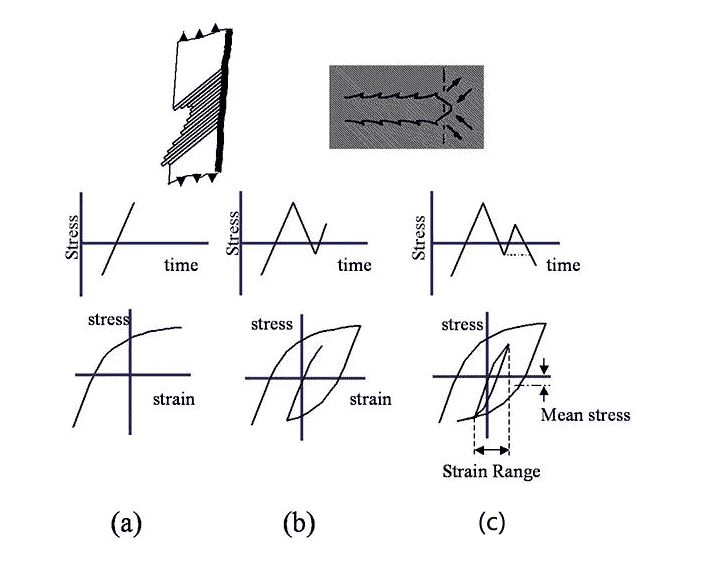
1Shear stress
From the diagram, we can see that a certain “amount” of shear stress is released during the periodic change of the strength of the nominal stress. And the larger the range of stress changes, the greater the energy released. Through the SN curve shown in Figure 1, we can see that the fatigue life decreases exponentially with the increase of the stress cycle range.
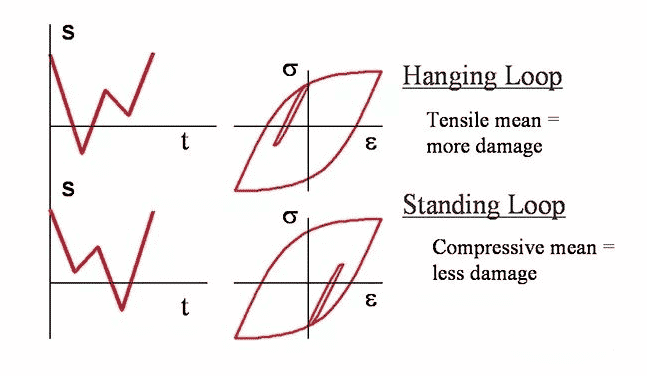
2 average stress
The average stress (residual stress) is also a factor affecting the fatigue failure rate. Conceptually, if the expansion stress is applied to the phase II crack, the crack will be forced to open, so any stress cycle will have a more significant effect. On the contrary, if the average compressive stress is applied, the crack will be forced to close, and any stress cycle needs to overcome the pre compressive stress before the crack can continue to expand. Similar concepts also apply to stage I cracks.
3 surface finish
Because fatigue cracks usually first appear on the surface of components where there are defects, the quality of the surface will seriously affect the probability of crack occurrence. Although most of the material test samples have mirror finish, so they will also achieve the best fatigue life. In fact, most components cannot be compared with the samples, so we need to modify the fatigue properties. Surface finish has a greater effect on the fatigue of components subjected to low amplitude stress cycles.
4 surface treatment
Surface treatment can be used to enhance the fatigue resistance of components. The purpose of surface treatment is to form residual compressive stress on the surface. Under the low amplitude period, the stress on the surface is obviously low, and even maintains the compressive state. Therefore, the fatigue life can be significantly prolonged. However, as we pointed out, this situation is only valid for components subject to low amplitude stress cycles. If a high amplitude period is applied, the pre compression will be overcome by the high amplitude period, and its advantages will be lost. As with surface quality, the impact of surface treatment can be shown by modeling.