¿Por qué el módulo de Young casi no se ve afectado por los 3 factores: composición del material, microestructura y estado de procesamiento?

Para conocer bien el módulo de Young y responder a esta pregunta en la barra de título, debemos pensar en cómo los materiales adquieren elasticidad.

En el caso de los materiales metálicos, sabemos que su interior está compuesto de átomos, muchos átomos están dispuestos regularmente para formar cristales y muchos granos se combinan para formar el metal que solemos ver.

¿La elasticidad proviene de la interacción entre los granos? Obviamente no, porque tanto el monocristalino como el amorfo tienen elasticidad.

Por lo tanto, la elasticidad probablemente proviene de la interacción entre los átomos.

Para ser lo más simple y conveniente posible, tratamos de no introducir conceptos complejos o fórmulas matemáticas. Comencemos con el modelo diatómico más simple.

Modelo diatómico del módulo de Young

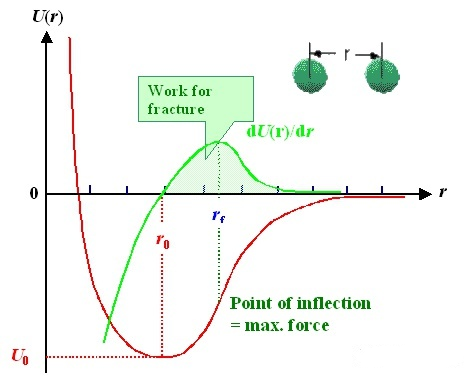
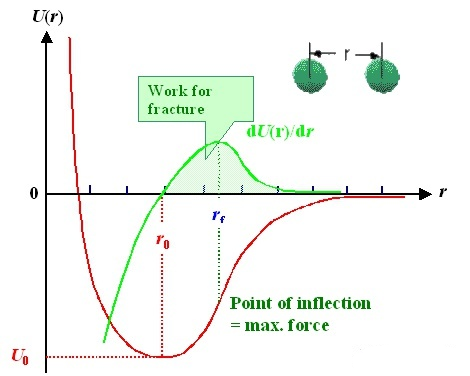
Modelo diatómico: la interacción entre dos átomos se puede describir mediante una función potencial (línea roja). El eje horizontal es la distancia “r” entre dos átomos, y el eje vertical es la energía potencial U (r); La fuerza de interacción (línea verde) se puede obtener derivando la función potencial. Vale la pena señalar que existe una posición de equilibrio r0r_ {0} entre los dos átomos, donde la fuerza de interacción F = 0 y la energía potencial es la más baja; En otras palabras, cuando dejes esta posición. No importa a la izquierda o a la derecha, habrá una fuerza tratando de hacerlo retroceder.

Como un resorte, existe tal posición de equilibrio en el estado natural. No importa si está apretando o estirando el resorte, que aún rebota a la posición original después de soltar la mano.

¡Esta es la fuente de elasticidad desde el nivel atómico!

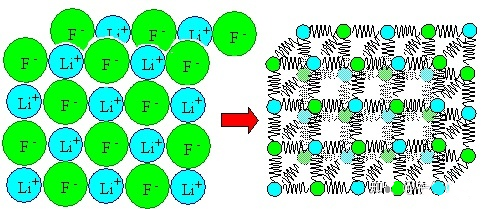
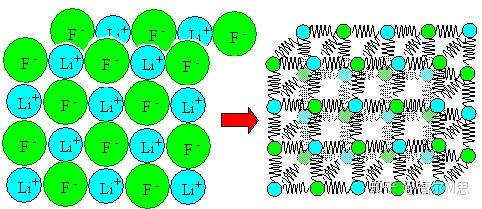
Por supuesto, los metales reales u otros materiales tienen muchos átomos en su interior. Estas interacciones atómicas pueden entenderse simplemente como la superposición de un par de interacciones atómicas.

análisis de la relación entre el módulo de Young y otros parámetros

En general, podemos simplemente suponer que esta función potencial tiene la siguiente forma:

La función anterior tiene cuatro parámetros variables, que son la posición de equilibrio R0R_{0}, Energía de oferta U0U_{0}y parámetros N y M. Los parámetros anteriores pueden variar para diferentes tipos de átomos.

Ahora tomamos estos dos átomos como un sistema independiente y los estiramos o comprimimos.

Para cambiar la distancia entre dos átomos cerca de la posición de equilibrio, la fuerza F que se debe aplicar

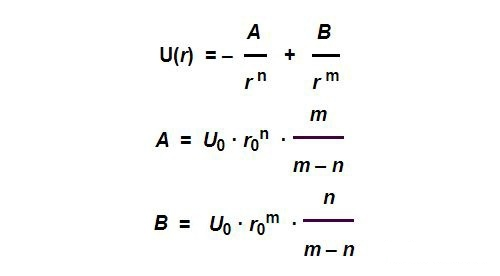
Para corresponder al módulo de Young, necesitamos cambiarlo a la Forma σ= E ε, dividir por uno r02r en ambos lados_ {0} ^ {2} y sustituir la fórmula anterior y pretender operar:

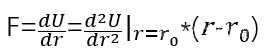
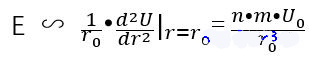
Conclusión

Es decir, el módulo de Young E se ve afectado principalmente por N, m, u0u_ {0}、r0r_ {0}. Las especies atómicas y la temperatura pueden afectar estos parámetros. La influencia de diferentes especies atómicas es obvia y todos los parámetros cambiarán. El efecto de la temperatura parece menos obvio.

Para observar el efecto de la temperatura, tenemos que volver a la propia curva de la función potencial. Debido a que la función potencial no es una curva simétrica perfecta, cuando la temperatura aumenta, significa que el átomo se mueve más vigorosamente y el rango de movimiento se vuelve más grande, como la expansión térmica y la contracción en frío. En este momento, la posición de equilibrio r0r_ {0} se compensará, como lo muestra la línea verde en la siguiente figura.

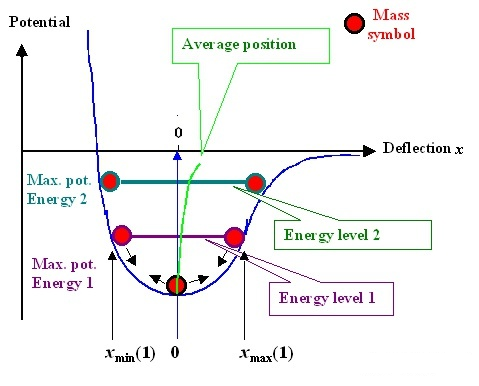
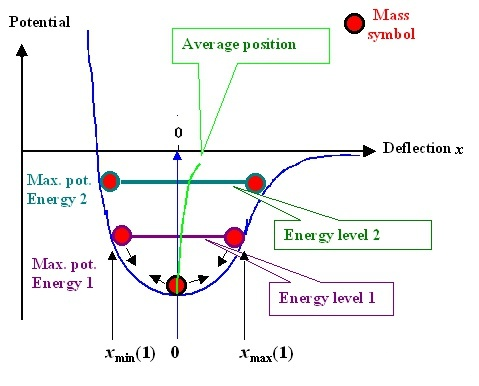
Se puede demostrar que los átomos siempre están en movimiento. Cuando la temperatura es alta, la posición de equilibrio r0r_ Cuanto mayor sea {0}, el volumen del material aumenta y el módulo de Young disminuye.

Volviendo a nuestra pregunta inicial, la cantidad de átomos de hierro en diferentes grados de acero puede representar más de 90%. Incluso en comparación con el hierro puro, la fuerza de interacción entre los átomos no cambia mucho, por lo que el módulo de Young apenas se ve afectado por el cambio de composición de la aleación; De manera similar, sin importar los cambios en la microestructura o el endurecimiento por trabajo, la reorganización de los átomos no cambia la fuerza entre los átomos, por lo que no afectan el módulo de Young.

Además del módulo de Young, también se pueden derivar de este modelo cantidades físicas como el punto de fusión, el coeficiente de expansión térmica y la resistencia a la tracción del cristal perfecto.

En cuanto al fenómeno anormal de que el módulo joven del caucho en alto estado elástico aumenta con el aumento de la temperatura, se debe a que la fuente de elasticidad del caucho es diferente de la de los materiales convencionales.