Le premier principe est en fait un terme philosophique avancé par le philosophe grec Aristote: il y a une proposition de base dans chaque système, qui ne peut être violée ou supprimée.Le premier principe est en fait un terme philosophique avancé par le philosophe grec Aristote: il y a une proposition de base dans chaque système, qui ne peut pas être violée ou supprimée.
Figure 1 Aristote

Dans le domaine de la science des matériaux, le premier principe se réfère au principe de l'interaction noyau atomique et électron et à sa loi de mouvement de base. En utilisant la mécanique quantique, à partir des exigences spécifiques, après une série d'approximations, l'équation d'onde de Schrodinger est directement résolue pour obtenir la structure électronique. Ainsi, les propriétés physiques et chimiques du système sont obtenues avec précision, et l'état et les propriétés du système microscopique sont prédits. Cependant, le processus de solution est très difficile. Pour cette raison, Born-Oppenheimer a proposé une approximation adiabatique, qui consiste à considérer l'ensemble du problème dans le mouvement des électrons et des noyaux. Compte tenu du mouvement du noyau à la position instantanée, compte tenu du mouvement du noyau, l'électron n'est pas pris en compte. La répartition spécifique de l'espace. Pour les systèmes à N électrons, la solution est toujours très difficile, donc une approximation à un seul électron est proposée, c'est-à-dire qu'un seul électron est considéré, et les autres électrons sont traités de manière similaire à une certaine forme de champ potentiel, qui est converti en un seul le problème électronique est l'approximation du champ moyen [1, 2].
Le premier principe consiste à résoudre l'équation de Schrödinger décrivant la loi de mouvement des particules microscopiques par calcul auto-cohérent sur la base d'une approximation adiabatique et d'une approximation à un seul électron. L'approximation de Hartree-Fock est une sorte d'approximation du champ moyen qui ignore l'interaction entre les électrons et traite les électrons comme des mouvements dans le champ potentiel moyen du champ potentiel ionique et d'autres électrons. L'approximation limite la précision du calcul. En 1964, Hohenberg et Kohn ont proposé une théorie fonctionnelle de la densité, qui exprime subtilement le potentiel lié à l'échange entre les électrons comme une forme de densité fonctionnelle, afin que les propriétés du matériau puissent être déterminées à partir de la densité électronique. Depuis lors, Kohn et Sham (Shen Lujiu) ont obtenu l'équation à un seul électron dans la théorie fonctionnelle de la densité, à savoir l'équation Kohn-Sham (KS), qui rend la théorie fonctionnelle de la densité pratiquement appliquée [3, 4]. Cet article résume les derniers progrès de l'application des premiers principes sous les aspects suivants:
Calcul des paramètres et de la configuration de la structure cristalline
La structure cristalline est la base pour comprendre les propriétés les plus fondamentales des matériaux, en particulier pour révéler la relation entre la microstructure des matériaux et les propriétés intrinsèques de l'élasticité, des électrons, des phonons et de la thermodynamique.
Leineweber et T. Hickel et al. utilisé la méthode exhaustive pour effectuer le calcul DFT sur les structures possibles de Fe4N et Fe4C, en tenant compte de l'arrangement fcc des atomes de Fe et de la position des atomes N / C sur les octaèdres, où une partie de la structure peut passer Bain. La distorsion devient stable, et l'atome C présente une séquence de type Zener en cc, comme le montre la figure 2, et révèle la différence caractéristique de la tendance d'orientation des atomes interstitiels, qui est cohérente avec la différence de structure austénitique observée expérimentalement [5 ].
Figure 2 Disposition fct (tétragonale centrée sur la face) de deux atomes de Fe (bleu)
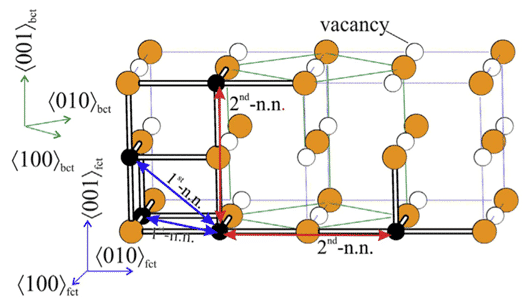
Calcul de la stabilité de la phase d'alliage
La méthode des premiers principes d'énergie totale basée sur l'onde plane super-potentiel est utilisée pour étudier la structure de la phase cristalline, et la stabilité thermodynamique de la microstructure des différents ordres d'empilement est obtenue, de sorte que la structure la plus stable qui puisse exister être un nouveau design et développement. Un moyen important de matériaux.
Par exemple, Zhilin Li, Chunyang Xia et al. a mené une étude de premier principe sur la stabilité de phase de Cu2ZnSnS4, un matériau de couche d'absorbeur de cellules solaires à couche mince, basée sur la théorie de la densité fonctionnelle (DFT), en utilisant PBE sous approximation de gradient généralisée (GGA). Les paramètres du réseau et l'énergie totale du système d'alliage Cu-Zn-Sn-S ont été calculés par le potentiel de corrélation d'échange, et le modèle de calcul et l'énergie de génération des phases possibles dans l'alliage Cu-Zn-Sn-S ont été établis. Les résultats sont présentés sur la figure 3 et le tableau 1. Comme indiqué, cette étude fournit des conseils pour la conception d'alliages Cu-Zn-Sn-S pour les cellules solaires composites à couches minces. Le modèle et la méthode de calcul peuvent également être étendus à la prévision de la stabilité de phase d'autres systèmes d'alliages [6].
Fig.3 Modèle de structure super-réseau de 64 défauts de substitution ZnCu
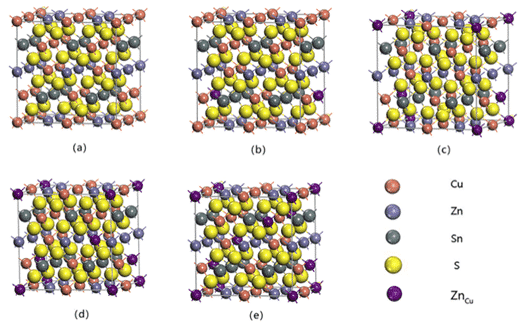
Tableau 1 Structure de super-réseau optimisée et résultats de calcul de l'énergie totale
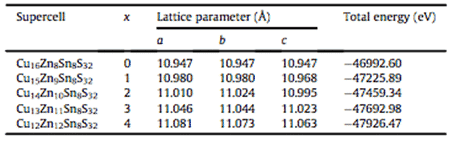
Structure électronique
Pour les structures stables, le calcul de la distribution de densité électronique de valence des matériaux est important pour comprendre le degré de liaison et d'ionisation entre les atomes.
Benkabou et H. Rached et al. a utilisé le premier principe pour calculer les alliages quaternaires CoRhMnZ (Z = Al, Ga, Ge et Si) Heusler (une classe de composés intermétalliques, qui peut être décrite comme X2YZ ou XX0YZ, où X, X0 et Y est un élément de métal de transition, Z est un élément du groupe III, IV ou V, contient généralement des éléments non ferromagnétiques, mais le composé présente une structure électronique ferromagnétique, calculée à l'aide de la méthode des ondes planes fixées linéaires à plein potentiel (FLAPW) et de l'approximation GGA-PBE. La figure 4 montre les résultats des calculs de densité d'état pour les structures correspondantes, montrant que ces composés présentent des ferromagnétiques semi-métalliques dans quelques états, les composés CoRhMnGe et CoRhMnSi et leurs moments magnétiques sont fondamentalement compatibles avec la loi de Slater-Pauling, indiquant leur semi-métallique Propriétés. Polarisation de spin élevée, en plus de CoRhMnSi, ces composés sont stables dans la structure YI [7].
Fig.3 Densité totale et densité locale des états des structures stables CoRhMnZ (Z = Al, Ga, Ge et Si)
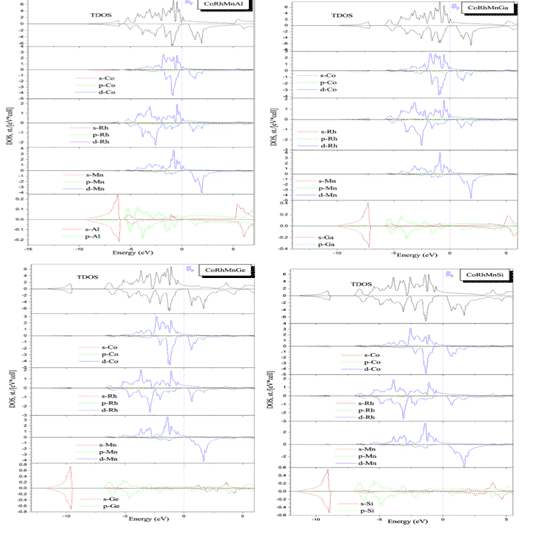
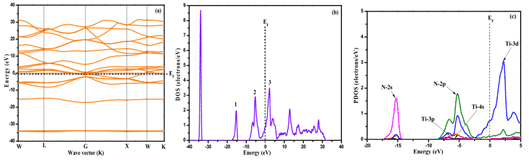
Song et al. a utilisé le premier principe pour étudier la structure électronique du film TiN. Comme le montre la figure 4, la bande a été simulée par le programme Studio Studio (MS) et la densité totale des états (DOS), la fonction diélectrique et l'absorption ont été calculées. Et la réflectivité.
Les résultats montrent que l'énergie de Fermi (EF) traverse la bande d'énergie avec une distribution de niveau d'énergie dense, et la densité totale des états croise avec EF, indiquant que TiN est déterminé par les propriétés électroniques de l'état Ti-3d pour avoir des propriétés métalloïdes [8 ].
Fig.4 Structure de la bande d'énergie du film de TiN (a), pleine densité (b) et densité locale (c)
Calcul des propriétés mécaniques
La constante élastique Cij est un paramètre de base décrivant les propriétés mécaniques des matériaux. Il est étroitement lié aux phénomènes solides de base, tels que la liaison interatomique, les équations d'état et les spectres de phonons, ainsi qu'aux propriétés thermodynamiques telles que la chaleur spécifique, la dilatation thermique, la température de Debye et les paramètres de Grüneisen. Lié. Théoriquement, il existe 21 constantes élastiques indépendantes Cij, mais la symétrie du cristal cubique réduit cette valeur à seulement 3 (C11, C12 et C44), et le module de cisaillement G, le module de Young E et Poisson sont dérivés des constantes élastiques. Rapport n, puis estimer la température de Debye à partir de la vitesse moyenne du son Vm :
Où H est la constante de Planck, KB est la constante de Boltzmann, Va est le volume atomique et Vm peut être déterminé par les vitesses sonores longitudinales et latérales vl et vt obtenues par le module de cisaillement G et le module de masse B dans l'équation de Navier. .
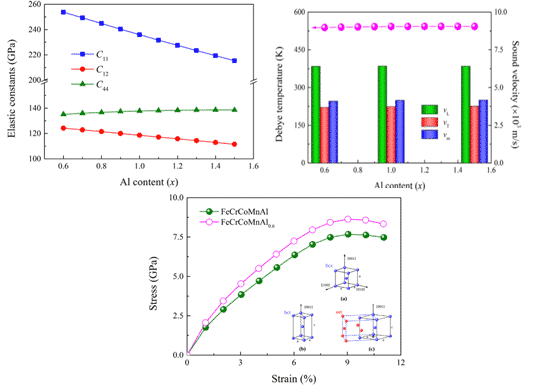
Par exemple, Shuo Huang et al. a combiné le premier principe pour déterminer les paramètres élastiques et la résistance à la traction idéale de la phase de solution solide cubique centrée sur le corps en alliage à haute entropie FeCrCoMnAlx (0,6≤≤1,5) dans la direction [001]. Les résultats sont présentés sur la figure 5. Dans la plage de composition considérée, la structure bcc s'est avérée avoir une énergie inférieure aux états ferromagnétique et paramagnétique des structures fcc et hcp. Sur la base de la température théorique de Curie, tous les alliages devraient être ferromagnétiques à température ambiante, et la résistance à la traction idéale dans la direction [001] devrait être de 7,7 GPa à une déformation maximale d'environ 9%. La résistance peut être encore augmentée en abaissant la concentration d'Al. [9].
Fig.5 Constante élastique, température de Debye et courbe contrainte-déformation de l'alliage à haute entropie FeCrCoMnAlx
Calcul des propriétés de surface ou d'interface
Récemment, Yu Lu et al. utilisé du métal d'apport de brasage composite Sn9Zn-1Al2O3-xCu pour braser l'alliage d'aluminium 6061, et étudié l'effet de l'ajout d'élément Cu et de particules Al2O3 sur les performances de brasage. Sur la base de la théorie de la théorie fonctionnelle de la densité (DFT) et du GGA-PBE, les calculs des premiers principes ont été effectués sur la structure interfaciale, l'énergie interfaciale, l'angle de contact et les propriétés électroniques de Al2O3 / Sn9Zn. Les calculs montrent que Sn9Zn-1Al2O3-4.5Cu et Sn9Zn-1Al2O3-6Cu ont une structure stable, et les résultats correspondants sont présentés sur les figures 6 et 7 [10].
Figure 6. Plans de contour avec différentes différences de densité de charge pour différentes structures: (a) Sn9Zn — 1Al2O3 , (b) Sn9Zn — 1Al2O3-4.5Cu
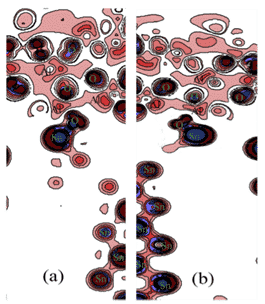
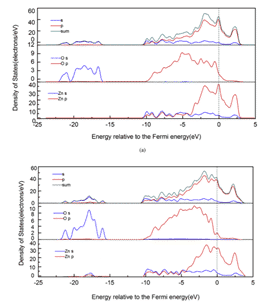
Figure 7 Densité d'état localisée de différentes structures: (a) Sn9Zn-1Al2O3, (b) Sn9Zn-1Al2O3-4.5Cu
Autres applications
Par exemple, Kulwinder Kaur et al. utilisé la théorie fonctionnelle de la densité (DFT) et la théorie de la transmission de Boltzmann pour étudier les propriétés thermoélectriques à haute température du fcc HfRhSb. Les figures 8 et 9 montrent la structure de la bande d'énergie calculée et la densité des états, ainsi que certains paramètres physiques. La théorie des caractéristiques de transmission commence par le calcul de la structure de la bande, la théorie de la transmission de Boltzmann dans la bande rigide et l'approximation du temps de relaxation constant (RTA). L'approximation de la bande de performance rigide (RBA) est un outil efficace pour étudier la relation entre la structure de la bande et la réponse thermoélectrique [11].
Figure 8 (a) structure de la bande d'énergie (b) densité de l'état local complet (c) dispersion des phonons (d) phonon DOS
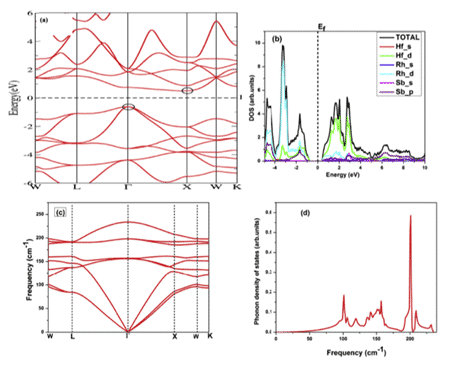
Figure 9 Coefficient de Seebeck, conductivité, conductivité thermique et efficacité thermoélectrique ZT en fonction de la température

Référence
1. Heisenberg W. Réinterprétation quantique-théorique des relations cinématiques et mécaniques [J]. Z Phys, 1925, 33: 879
2.Schrodinger E, Quantisierung als eigenwertproblem I [J]. Ann der Phys, 1926, 9: 361
3. Hohenberg P, Kohn W. Gaz d'électrons inhomogène [J]. Phys Rev B, 1964, 136 (3): 864
4.Kohn W, Sham L J. Équations auto-cohérentes, y compris les effets d'échange et de corrélation [J]. Phys Rev A, 1965, 140 (4): 1133
5. Leineweber, T. Hickel, B. Azimi-Manavi, SB Maisel structures Structures cristallines de Fe4C vs Fe4N analysées par les calculs DFT: les superstructures interstitielles basées sur Fcc explorées [J], Acta Materialia 140 (2017) 433-442
6.Zhilin Li, Chunyang Xia, Zhengping Zhang, Meiling Dou, Jing Ji, Ye Song, Jingjun Liu, Feng Wang , Première étude de principe sur la stabilité de phase de la kestérite Cu2ZnSnS4 pour les cellules solaires à couche mince avec une composition hors stœchiométrique [J] , Journal des alliages et composés 768 (2018) 644-651
7.Benkabou, H.Rached, A. Abdellaoui, D.Rached, R. Khenata, MH Elahmar, B. Abidri, N. Benkhettou, S.Bin-Omran , Structure électronique et propriétés magnétiques des alliages quaternaires Heusler CoRhMnZ (Z = Al, Ga, Ge et Si) via des calculs de premier principe [J] , Journal of Alloys and Compounds 647 (2015) 276-286
8. Huijin Song, Peng Gu, Xinghua Zhu, Qiang Yan, Dingyu Yang , Étude de la structure électronique et des propriétés optiques des films TiN basée sur le premier principe [J] , Physica B: matière condensée 545 (2018) 197-202
9. Huo Huang, Xiaoqing Li, He Huang, Erik Holmstro € m, Levente Vitos, Performances mécaniques des alliages à haute entropie FeCrCoMnAlx du premier principe [J], Chimie des matériaux et physique 210 (2018) 37-42
10.Yu Lu, Le Ma, Shu-yong Li, Wei Zuo, Zhi-qiang Ji, Min Ding , Effet de l'addition d'éléments Cu sur le comportement interfacial et les propriétés mécaniques des alliages d'aluminium 6061 Sn9Zn-1Al2O3 à souder: calculs de premier principe et recherche expérimentale [J] , Journal of Alloys and Compounds 765 (2018) 128-139
11.Kulwinder Kaur, Ranjan Kumar, DP Rai, Une réponse thermoélectrique prometteuse du composé HfRhSb demi Heusler à haute température: une première étude de principe [J], Journal of Alloys and Compounds 763 (2018) 1018-1023







