ヤング率をよく知り、タイトル バーのこの質問に答えるには、材料がどのように弾性を得るかを考える必要があります。
金属の物質は、その内部が原子で構成されており、多くの原子が規則的に配列して結晶を形成し、多くの粒子が結合して私たちが普段目にする金属を形成していることがわかっています。
弾力性は粒子間の相互作用から来るのですか?単結晶もアモルファスも弾性を持っているからです。
したがって、弾性はおそらく原子間の相互作用に由来します。
できるだけシンプルで便利にするために、複雑な概念や数式を導入しないようにしています。から始めましょう 最も単純な二原子モデル.
ヤング率の二原子モデル
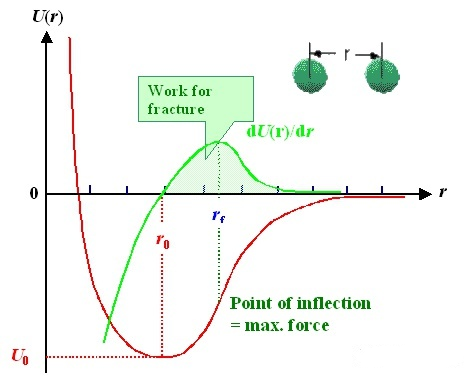
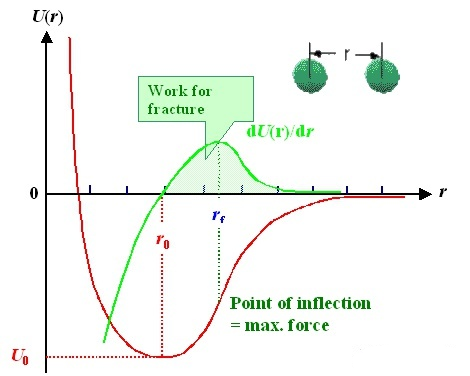
2 原子モデル: 2 つの原子間の相互作用は、ポテンシャル関数 (赤い線) によって記述できます。横軸は 2 つの原子間の距離「r」、縦軸はポテンシャルエネルギー U (r) です。相互作用力(緑線)は、ポテンシャル関数を導出することで得られます。 2 つの原子の間に r0r_ {0} という平衡位置があり、相互作用力 F = 0 であり、ポテンシャル エネルギーが最小であることは注目に値します。つまり、この位置から離れると、左右どちらに傾いても引き戻そうとする力が働きます。
バネのように、自然な状態でこのようなバランス位置があります。スプリングを握っても伸ばしても、手を離すと元の位置に戻ります。
これが原子レベルの弾力の源!
もちろん、実際の金属やその他の物質には多くの原子が含まれています。これらの原子相互作用は、一対の原子相互作用の重ね合わせとして簡単に理解できます。
ヤング率と他のパラメータとの関係の分析
一般に、この潜在的な関数は次の形式を持つと単純に仮定できます。
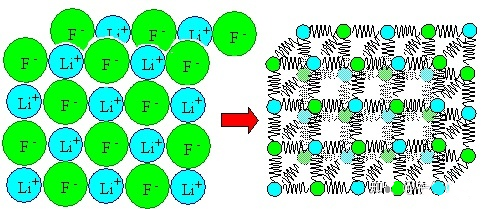
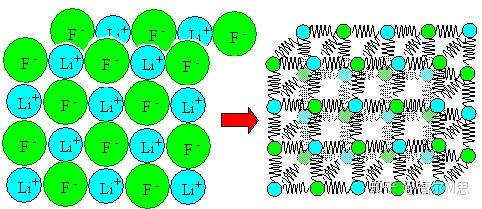
上記の関数には、平衡位置 R0R_ である 4 つの変数パラメーターがあります。{0}、結合エネルギー U0U_{0}、パラメータ N および M。上記のパラメータは、原子の種類によって異なる場合があります。
ここで、これら 2 つの原子を独立したシステムとして取り、それらを伸ばしたり圧縮したりします。
平衡位置付近で 2 つの原子間の距離を変えるために、加える力 F
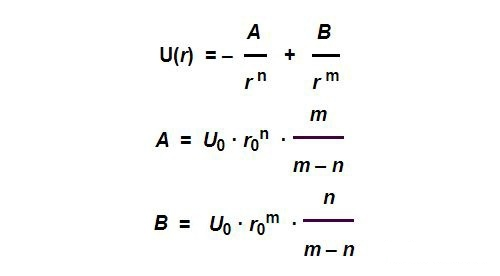
ヤング率に対応させるには、σ= E ε の形に変えて、両辺を r02r で 1 で割る _ {0} ^ {2} と上記の式を代入して、
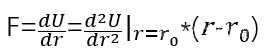
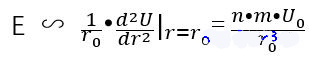
結論
つまり、ヤング率 E は主に N, m, u0u_ {0}、r0r_ {0} の影響を受けます。原子種と温度は、これらのパラメーターに影響を与える可能性があります。異なる原子種の影響は明らかで、すべてのパラメータが変化します。温度の影響はそれほど明らかではないようです。
温度の影響を観察するには、ポテンシャル関数曲線自体に戻る必要があります。ポテンシャル関数は完全な対称曲線ではないため、温度が上がると原子はより活発に動き、熱膨張や冷間収縮などの可動域が大きくなることを意味します。このとき、バランス位置 r0r_{0} は下図緑線のようにずれます。
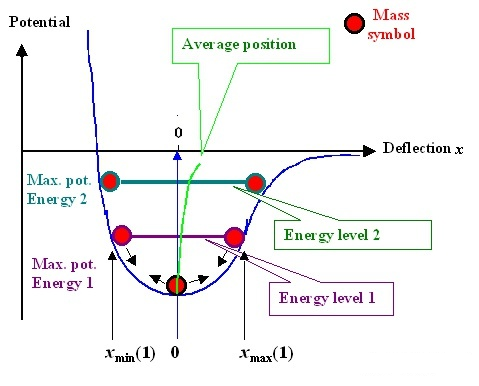
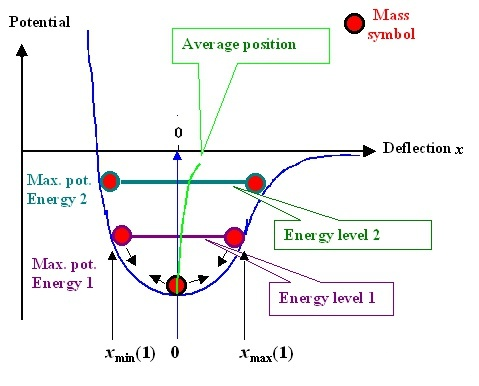
原子が常に動いていることは証明できます。温度が高い場合、平衡位置 r0r_ {0} が大きいほど、材料の体積が増加し、ヤング率が減少します。
最初の質問に戻ると、さまざまなグレードの鋼に含まれる鉄原子の数は、90% を超える可能性があります。純鉄と比較しても原子間の相互作用力は大きく変わらないため、ヤング率は合金組成の変化の影響をほとんど受けません。同様に、微細構造の変化や加工硬化に関係なく、原子の再配列は原子間の力を変化させないため、ヤング率には影響しません。
ヤング率に加えて、融点、熱膨張係数、完全結晶の引張強度などの物理量もこのモデルから導き出すことができます。
高弾性状態のゴムが温度上昇とともにヤング率が上昇するという異常現象は、従来の材料とはゴム弾性の源泉が異なるためです。







