部品のポイントに十分な外乱応力が加わると、十分なサイクル数後にクラックが発生し、これを疲労と呼びます。疲労破壊は、エンジニアリング構造とコンポーネントの故障の主な原因です。現在のアプリケーションと研究では、疲労試験方法には主に4つのタイプがあります。
1.公称応力およびひずみ法。
2.局所応力およびひずみ法。
3.エネルギー法。
4.破壊力学法。
この記事では、4種類のメソッドとそのアプリケーションについて簡単に紹介します。
1.公称応力法
公称応力法は、標準部品に定格応力試験を適用する方法であり、最大繰返し応力と降伏応力の関係から、応力疲労とひずみ疲労に分類されます。
まず、応力疲労が導入されます。これは、最大周期応力Smaxが降伏応力Syより小さい場合の応力疲労として定義されます。応力疲労試験により、材料寿命は104倍以上あるため、応力疲労は高サイクル疲労とも呼ばれます。応力疲労の理論によれば、金属材料の応力Sと破損のサイクル数Nは非線形に分布します。利用可能なべき関数:対数を取る:、または指数関数を使用する:対数を取ることで表現します。この方法はSN法と呼ばれます。結果は、SNカーブ、または実際のテストのp(生存率)-SNカーブを使用して分析されました。
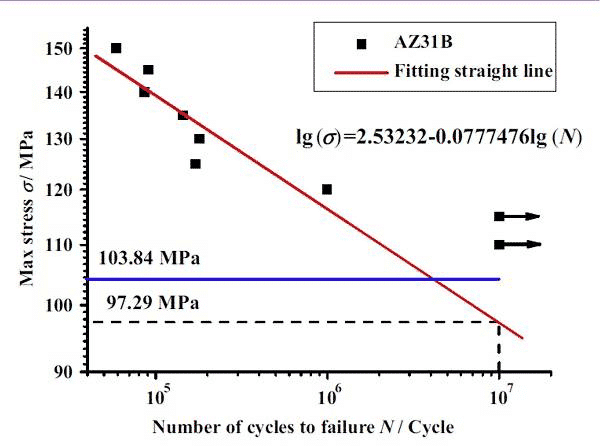
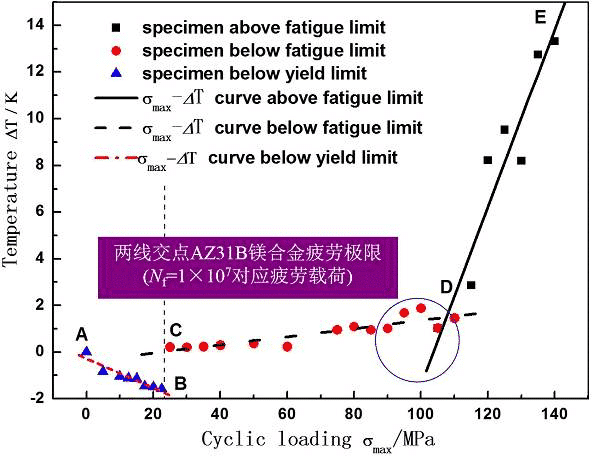
材料疲労SNカーブには、一般的に応力疲労が使用されます。図1および図2に示すように、AZ31Bマグネシウム合金の疲労限度(応力比は0.1、疲労寿命は疲労荷重に相当する107)は、リフティング法で試験されています。図のAZ31Bマグネシウム合金サンプルの疲労限度は97.29 MPaです。
図1. AZ31Bマグネシウム合金疲労試験

図2. AZ31Bマグネシウム合金疲労試験のSNカーブ
ひずみ疲労は、高負荷、低設計寿命のコンポーネントのテストに適用されます。定義は次のとおりです。最大周期応力Smaxが降伏応力Syよりも大きい場合、それはひずみ疲労です。応力疲労試験は、高負荷および低周波数でのコンポーネントの研究に使用されます。たとえば、圧力容器の耐用年数では、サイクルの合計数は104のオーダーです。したがって、疲労性能パラメータの記述としてひずみが使用されます。ストレス疲労は低サイクル疲労としても知られています。
ひずみ疲労研究の学者たちは、次の理論、材料の応力ひずみ(Remberg-Osgood弾塑性応力ひずみ)関係を提唱しています。
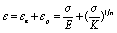
式では、εe弾性ひずみ振幅、εpは塑性ひずみ振幅です。
定振幅対称ひずみ試験では、材料の塑性変形により、ひずみが減少すると元の経路では応力を減少させることができず、応力-ひずみ曲線は環状になります。この曲線はヒステリシスループと呼ばれます。サイクル数が増加すると、同じひずみ振幅応力が増加または減少します。変化に対応するこの応力の応答は、循環硬化または循環軟化と呼ばれます。サイクルは数サイクルで十分であり、一部の材料は安定したヒステリシスループを形成します。
ひずみ疲労では、応力-ひずみ曲線を使用して、材料の循環硬化または循環軟化傾向を記述します。対称的なヒステリシスループ曲線を持つ材料の場合、これは質量材料と呼ばれます。
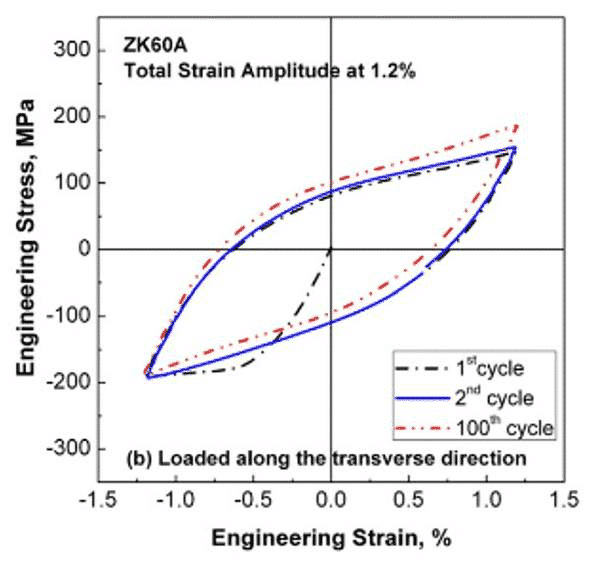
下の図は、圧延方向と横方向に荷重をかけたZK60マグネシウム合金のσ-ε曲線を示しています。横方向では、周期硬化現象が顕著です。
図3.σ-ε回転曲線に沿ったZK60Aマグネシウム合金荷重
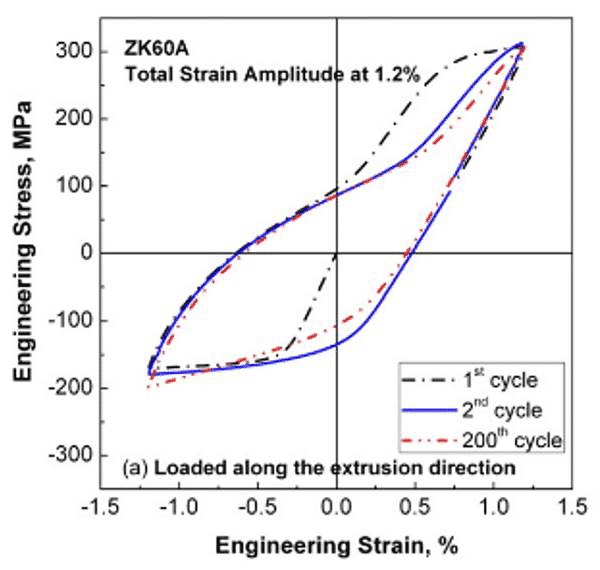
図4.横方向のσ-εカーブに沿ったZK60Aマグネシウム合金の荷重
2.局部応力およびひずみ法
切り欠きのある試験片と応力集中部品については、局部応力ひずみ解析が使用されます。現在の研究では、部材の疲労寿命は局所的な最大ひずみと応力であり、応力集中係数の概念が提案されています。材料の亀裂形成の寿命の計算や、コンポーネントの残留疲労寿命の予測に適しています。
局所応力法が提唱する理論は、ノイバーの公式(応力集中式)
Minner理論(疲労累積損傷理論):一定応力Sの下での部材の疲労寿命はNであり、nサイクルによる損傷は次のとおりです。
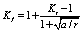
k一定応力Siの下でniサイクルにさらされた場合、合計損傷は次のように定義できます。
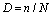
損傷基準は次のとおりです。
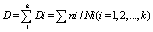
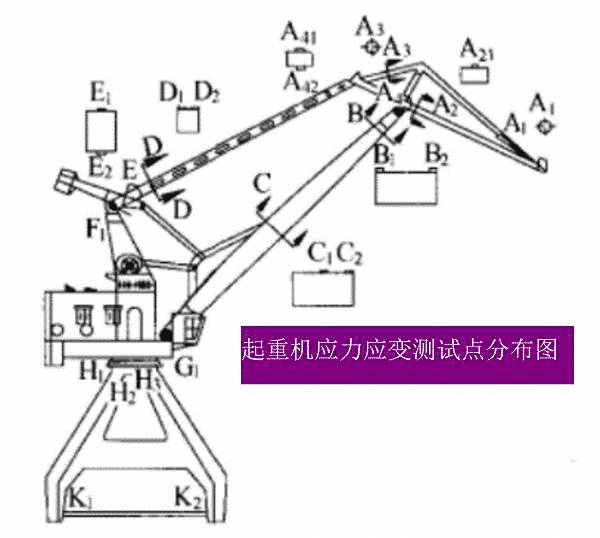
局所応力法の適用を図5と図6に示します。
図5.切欠き付き試験片の疲労寿命予測
図6.クレーンの疲労寿命予測(クレーンの応力とひずみのテストポイント分布マップ)
応力集中点の疲労寿命は、次の式に従って計算されます。
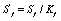
ここで: Sf – 等価応力平滑サンプル疲労寿命
図6クレーンの疲労寿命計算方法は、異なる試験点の時刻歴マップと各点の疲労寿命方程式を入力し、各点の残留疲労寿命を計算する方法です。デフォルトの寿命最小点は、デバイスの残りの疲労寿命です。クレーンの場合、学者たちは普通鋼の累積損傷値Dが0.68に達することを示唆しています。
3.エネルギー法
赤外線サーモグラフィーは、材料の疲労過程のエネルギー定数の法則に基づいて、疲労性能を予測する方法です。疲労熱画像法は、熱力学エネルギーU、運動エネルギーK、および疲労過程におけるエネルギー散逸の他の形態に基づいています。物体によって吸収または放散されるエネルギー変化Eと熱変化Qの合計は、物体に作用する仕事Wでなければなりません。同じ。
疲労熱画像処理には、非破壊、リアルタイム、非接触の利点があります。同時に、エネルギー散逸と疲労荷重の間の非線形関係、および熱散逸を使用した温度散逸の誤差のため、それはまだ工業的測定には適していません。
現在の研究では、次の予測モデル理論、Luong法、ΔTmax、および疲労寿命Nfが提案されています。
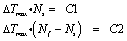
ここで、C1、C2は定数です。
したがって、疲労限度は2線法で予測できます。熱放散に基づいて、学者は次のモデルを提案しました:
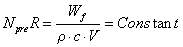
R温度上昇勾配
以下は、太原理工大学の張洪夏先生のチームによる疲労熱画像法の研究です。 AZ31B Mg合金の疲労寿命は、サーマルイメージングによってすぐに予測されました。 2行法に従って材料の疲労限度を予測するには、サンプルの最初の段階の温度上昇をテストするだけで済みます。それぞれ図7、図8、図9。
図7.疲労試験のサイクルタイムが異なるAZ31Bマグネシウム合金サンプルの表面温度
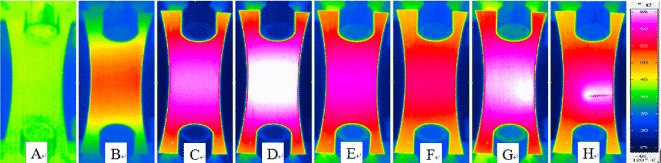
図8. AZ31B疲労プロセスのサンプル表面温度曲線
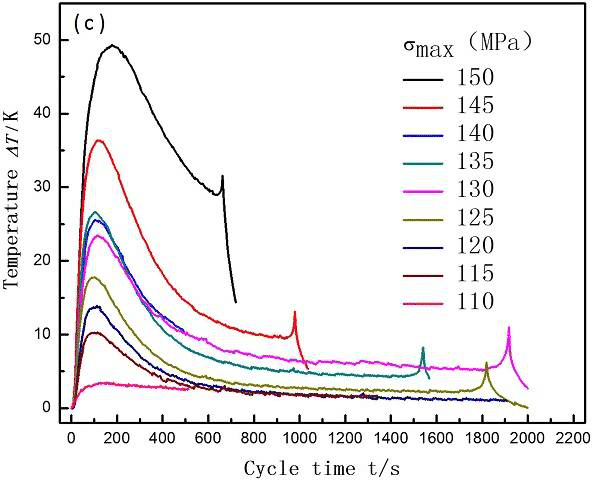
図9.疲労荷重による温度の変化
4.破壊力学法
線形弾性破壊力学は、疲労亀裂の成長を研究するための理論的な基礎です。疲労亀裂伝播は、応力拡大係数Kによって定量的に説明することもできます。
疲労荷重の下では、サイクル数Nによる亀裂長さaの変化率a、da / dNは、疲労き裂成長の速度であり、亀裂の伝播速度を反映しています。与えられた亀裂長さaに対して、da / dNは繰返し応力振幅∆σの増加に伴い増加します(∆σが大きいほど、∆Kは大きくなります)。この現象に基づいて、学者はda /dN-ΔK(亀裂伝播)を研究しています。レート-ストレス強度増加曲線、曲線は3つのゾーンに分割できます:低レート、中レート、高レートゾーン。パリの公式は、中程度のレートの安定した拡張の間には線形関係があると述べています:
亀裂先端の形状の実験式:
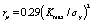
疲労亀裂の形成と膨張は、損傷力学の枠組みの下で統一することができます。
以下は、AZ31Bマグネシウム合金の亀裂成長速度の研究であり、AZ31Bの安定した膨張速度を評価します。
図10.疲労亀裂先端の競合メカニズムの概略図
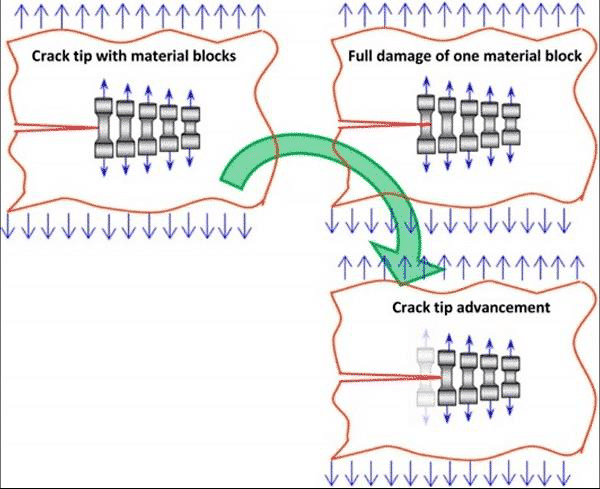
図11.亀裂先端の応力-ひずみ場の3つの異なる領域の概略図
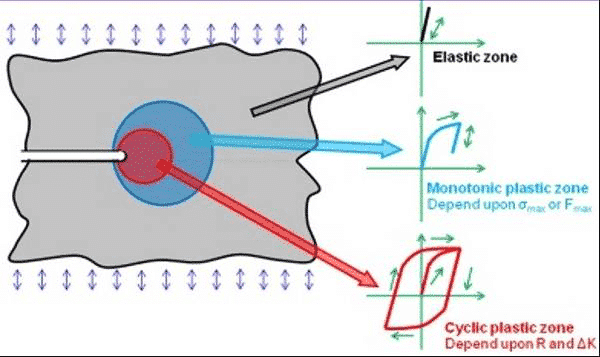
図12.疲労亀裂先端の競合メカニズムのaN曲線の概略図
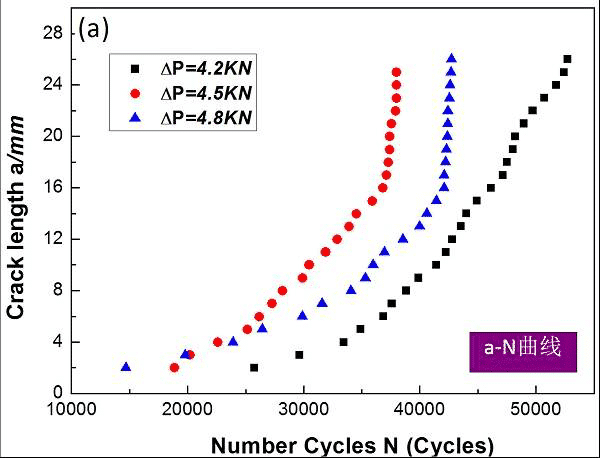
図13.疲労亀裂先端の競合メカニズムのda /dN-ΔK曲線の概略図
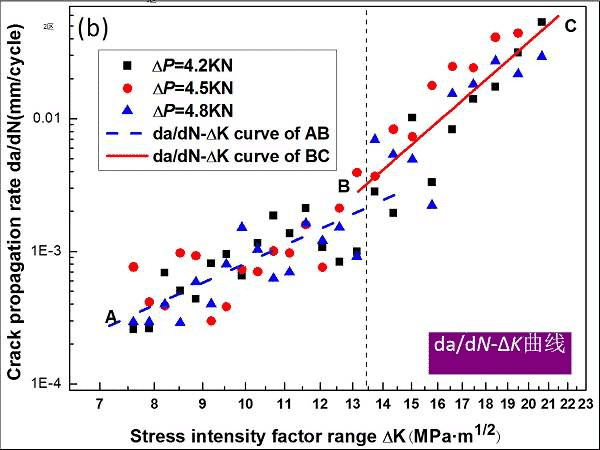
ABセグメント(中速帯):da / dN = 4.57×10-7(ΔK)3.25(7.2 <ΔK≦13.5 MPa•m1 / 2)
BCセグメント(高速ゾーン):da / dN = 3.16×10-10(ΔK)6.21(13.5 <ΔK≤22.1MPa•m1 / 2)
結論:
4つのタイプのメソッドは、アプリケーションが異なります。公称応力法と局所応力法は、産業分野における材料と部品の性能試験に適しています。エネルギー法は材料の疲労寿命を予測でき、破壊力学法は疲労亀裂の形成と膨張を統合することに成功しています。








