밀도 기능 이론 (DFT)은 응축 물질 물리학, 재료 과학, 양자 화학 및 생명 과학 분야에서 다중 입자 시스템을 다루기위한 근사법으로 널리 사용되었습니다. 예를 들어, 그림 1 (c)는 DFT 방법 [1]을 사용하여 계산 된 72 원자 슈퍼 셀 구조입니다. DFT 기반 재료 과학 계산 시뮬레이션 방법은 기존 재료를 연구 할 수있을뿐만 아니라 새로운 재료를 예측할 수도 있습니다.
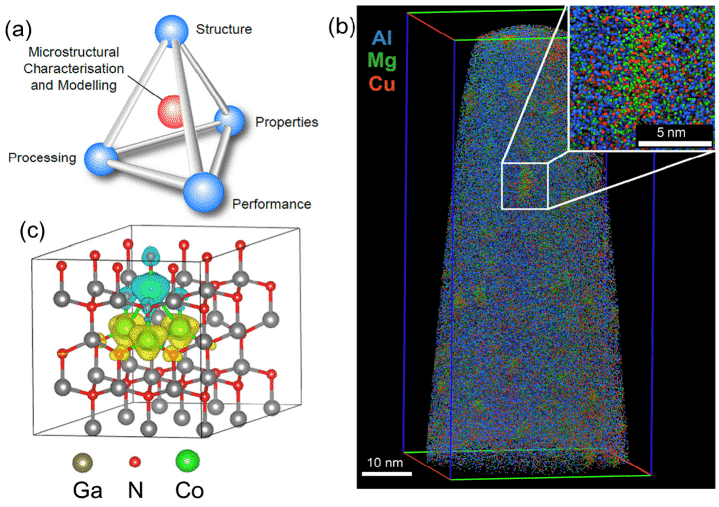
그림 1 (a) 미세한 특성화, 구조, 가공, 특성 및 특성 간의 잠재적 연관성, (b) 약 2 천만 개의 원자를 포함하는 Al-Cu-Mg 합금에 대한 APT 데이터, (c) DFT 계산을위한 72- 원자 슈퍼 셀 예
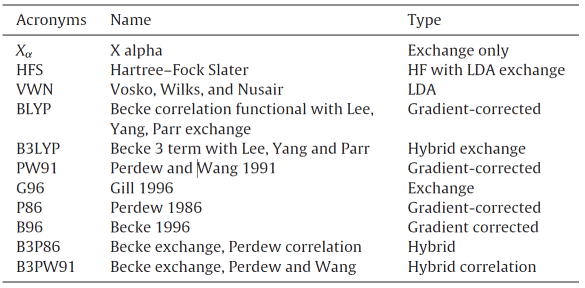
함수는 벡터 공간에서 스칼라로의 함수, 함수의 함수입니다. 표 1은 제안 된 밀도 함수의 일부 유형을 나열하고 있으며, 그 중 일부는 기본 양자 역학에서 파생되고 일부는 고유 한 장단점과 적용 범위를 가진 파라 메트릭 함수에서 파생됩니다 [2]. DFT 방법의 본질은 전자 밀도를 단일 전자의 파동 함수가 아닌 분자 (원자) 접지 상태의 모든 정보의 캐리어로 사용하여 다중 전자 시스템을 단일 전자 문제. 전자의 개수가 N이라고 가정하면 파동 함수의 변수 개수는 3N이며 밀도 함수 이론은 변수 개수를 3 개의 공간 변수로 줄여 계산 프로세스를 단순화하고 계산 정확도를 보장합니다.
표 1 대략적인 밀도 기능 유형
밀도 기능 이론의 개발은 크게 세 단계로 나눌 수 있습니다. 첫 단계는 1927 년이었습니다. Thomas와 Fermi는 이상적인 조건에서 이상적인 전자 가스 가설을 기반으로 Thomas-Fermi 모델을 제안했습니다. 처음으로 밀도 기능 이론의 개념이 도입되었으며, 이는 이후 DFT 방법의 프로토 타입이되었습니다.
Thomas-Fermi 모델의 시작점은 전자 사이에 상호 작용이없고 외부 간섭이 없다고 가정하는 것입니다. 전자 운동에 대한 슈뢰딩거 방정식은 다음과 같이 표현할 수 있습니다.
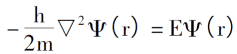
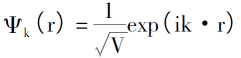
0K 이하의 전자 배열 법칙을 도입하면 전자 밀도, 단일 전자의 총 에너지 및 시스템의 운동 에너지 밀도는 다음과 같습니다.
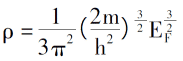
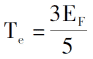
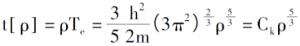
전자 사이의 쿨롱 전위 및 외부 필드에 대한 설명을 도입함으로써, 전자 밀도 함수에 의해서만 결정된 전자 시스템의 총 에너지 표현이 도출 될 수있다 [3].
모델은 계산 형태와 프로세스를 단순화하지만 전자 간의 상호 작용을 고려하지 않습니다. 운동 에너지 항목을 정확하게 설명하지 않으므로 많은 시스템에 적용 할 수 없습니다. 그러나이 새로운 연구 아이디어에서 영감을 얻은 관련 학자들은 기본적으로 수년간의 노력 끝에 1960 년대에 밀도 기능 이론의 내용을 완성했으며, 최종적으로 엄격한 밀도 기능 이론을 확립했습니다.
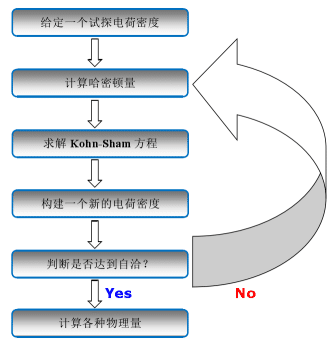
그림 2 DFT 기반의 일관된 반복 프로세스의 개략도
Hohenberg-Kohn 정리와 Kohn-Sham 방정식은 DFT 방법의 형성과 개선에 핵심적인 역할을했으며 DFT의 두 가지 초석으로 환영 받았습니다.
(1) 호헨 버그-콘 정리
Hohenberg-Kohn 정리의 핵심 아이디어는 시스템의 모든 물리량을 전자 밀도 만 포함하는 변수로 고유하게 결정할 수 있으며 구현 방법은 변동 원리를 통해 시스템의 접지 상태를 얻는 것입니다. 이 이론은 주로 불균일 전자 가스 모델을위한 것이며 두 개의 하위 정리로 구성됩니다. i) 전자 전위에 의해 외부 전위가 고유하게 결정될 수있는 외부 전위 (전자 상호 작용 이외의 전위)에서 스핀을 무시하는 전자 시스템; ii) 주어진 외부 전위에 대해 시스템 접지 상태 에너지는 에너지 기능 값의 최소값입니다. 따라서 시스템의 에너지 기능은 다음과 같이 설명 할 수 있습니다.
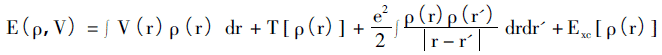
방정식의 오른쪽은 포텐셜 에너지, 운동 에너지 항, 전자 간의 쿨롱 상호 작용 및 외부 필드에서의 교환 관련 포텐셜 에너지입니다.
이 정리는 전자 밀도 함수, 운동 에너지 기능 및 교환 관련 기능의 특정 표현을 제공하지 않으므로 특정 솔루션은 여전히 가능하지 않습니다.
(2) 콘-샴 방정식
1965 년까지 Kohn과 Shen Lujiu는 Kohn-Sham 방정식을 수립하여 각 항목에 대한 자세한 설명을 제공했으며 밀도 기능 이론은 실제 적용 단계에 들어가기 시작했습니다. 그들은 운동 에너지 기능이 상호 작용없이 입자 운동 에너지 기능을 사용하여 치환을 근사하도록 제안했으며,이 둘 사이의 차이는 교환 관련 기능의 미지에 포함되어있다 [4]. Φi (r)의 변화, 및 라그랑주 승수는 Ei로 대체된다. 단일 전자 방정식은 다음과 같습니다.
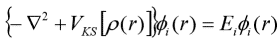
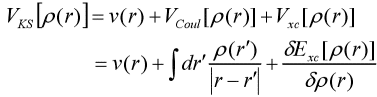
위는 n- 샴 방정식입니다.
Kohn-Sham 등식은 교환 관련 함수 외부의 모든 항목에 대해 명확한 표현을 제공하며 복잡한 효과를이 용어로 분류합니다. 이 시점에서 계산의 어려움이 크게 단순화되고 모든 작업은 교환 관련 기능 확장을 설명하는 방법에 대해 시작됩니다. 동시에, 교환 관련 전위의 대략적인 형태는 밀도 기능 이론의 정확성을 직접 결정합니다.
1965 년 Kohn and Shen Lujiu는 LDA (Local Density Approximation) 방법을 제안했습니다.이 목적은 알려지지 않은 교환 연결을 근사하여 DFT 방법을 실제 계산에 사용할 수 있습니다. LDA는 균일 한 전자 가스의 밀도 함수를 사용하여 불균일 한 전자 가스의 교환 관계를 계산합니다. 시스템의 전자 밀도가 공간에 따라 거의 변하지 않는다고 가정하면, 불균일 전자 가스의 교환 관계는 다음과 같이 표현 될 수 있습니다.
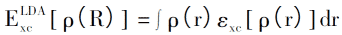
해당 교환 상관 전위는 다음과 같이 표현 될 수 있습니다.
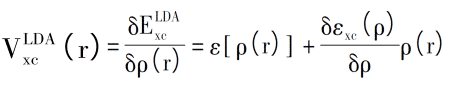
예를 들어, Asad Mahmood et al. VASP를 사용하여 LDA-PBE와 GGA-PAW 계산의 평형 구조 매개 변수를 비교하고, 전자 오비탈 혼성화에 대한 Ga 도핑의 영향뿐만 아니라 광학 특성 및 결정 형상을 그림 3 (c)에서 연구했습니다. Ga-2s와 Ga-2p 오비탈은 전도에 크게 기여하고, 낮은 VB는 Ga-2p에 의해 기여하며, CB 하단의 불순물 밴드는 추가적인 에너지 장벽, VB 사이의 전자를 나타냅니다. 그리고 CB. 전이는 에너지 장벽을 넘어야한다 [5].
그림 3 계산 결과
(a) 최적화 된 3x3x3 Ga- 도핑 된 ZnO 슈퍼 셀, (b) 대역 구조, (c) 밀도 DOS
실제 재료 시스템을보다 정확하게 계산하기 위해 1986 년 Becke, Perdew 및 Wang et al. 밀도 함수 계산에서 가장 널리 사용되는 처리 방법 인 GGA (Generalized Gradient Approximation)를 제안했습니다.
GGA 처리 방법은 원래의 표현을 전자 밀도 및 기울기 함수와 스핀에 대한 설명을 포함하는 기능 형태로 다시 작성하는 것이며, 그 결과 교환 관련 기능은 다음과 같습니다.
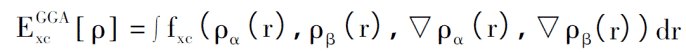
GGA에서 교환 상관 전위는 교환 에너지와 상관 에너지로 분해될 수도 있습니다. 그렇다면 이 두 부분에 대한 합리적인 표현을 어떻게 구성할 수 있을까요? Beckc et al. 구체적인 기능 형태는 원칙적으로 임의로 구성할 수 있으며 GGA-PW91과 같은 실제 물리적 의미를 고려할 필요가 없다고 생각합니다. Perdew et al. 최대한 순수한 양자역학 계산 이론으로 돌아가자고 주장하며 모든 물리량은 계산될 뿐입니다. 전자정적질량, 플랑크상수, 광속 등의 기본상수부터 시작하여, 함수식은 응축물 등의 분야에서 많이 사용되는 GGA-PBE(Perdew-Burke-Enzerhoff)와 같은 경험적 매개변수를 과도하게 포함해서는 안 된다. 물리학.
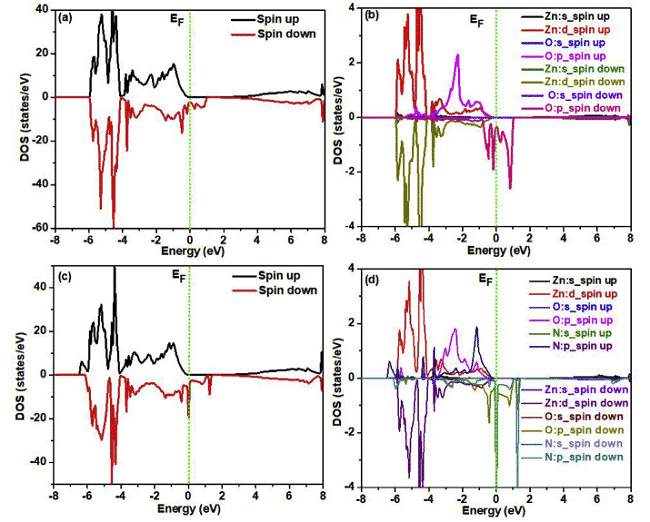
최근에 Parmod Kumar 및 L. Romaka et al. WIEN2k 및 Elk v2.3.22에서 각각 FP-LAPW (전위 선형 선형 강화 평면파)를 사용하여 관련 연구를 수행했으며, 여기서 교환 상관 전위는 GGA-PBE 형식입니다 (그림 4, 5). 상태 밀도 및 전하 밀도 분포 [6,7].
그림 4 N 주입 및 주입이없는 스핀 분극 ZnO 슈퍼 셀의 상태의 총 밀도 및 상태의 국소 밀도
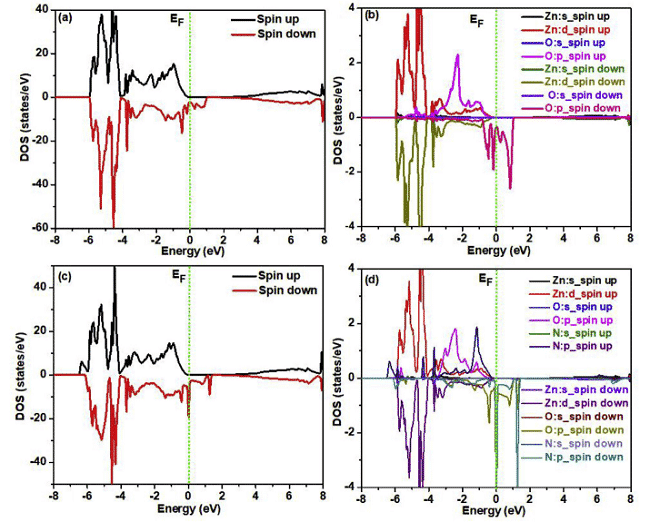
그림 5 VCoSb telluride J. Ibáñez, T. Woźniak et al.에서 전자 위치 결정 함수 분포 (Y)와 전하 밀도 (r). 압력 하에서 HfS2의 격자 역학을 예측하기 위해 다른 밀도 기능 이론의 유효성을 테스트했습니다.
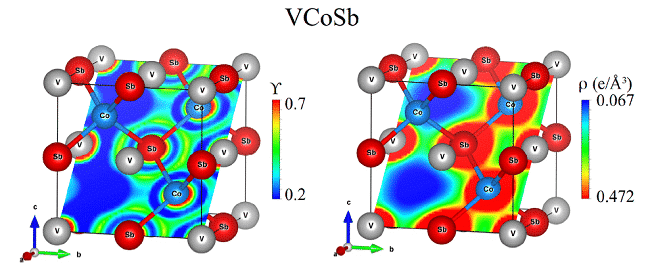
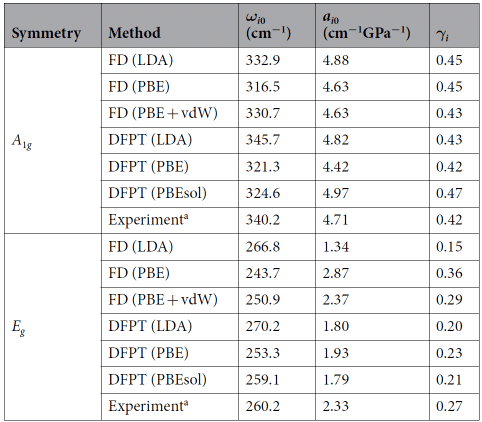
관찰 표 2는 GGA-DFT가 vdW 상호 작용을 고려하여 HfS2의 고압 격자 역학을 적절하게 설명하고 LDA-DFT 계산은 환경 조건 하에서 2D 화합물의 구조 및 진동 특성을 예측하는 데 널리 사용되며 압축 상태에서 재현 할 수 없음을 발견했습니다. 정황. HFTS2의 거동은 DFT-LDA를 사용하여 TMDC와 Grüneisen 매개 변수의 압축성을 계산할 때 큰 오류가 발생 함을 나타냅니다 [8].
표 2 라만 주파수 (ωi0), 압력 계수 (ai0) 및 Grüneisen 매개 변수 (γi)
LDA 및 GGA 알고리즘 외에도, 1998 년에 널리 사용되었던 B3LYP와 같은 하이브리드 방식으로 Hatree-Fock (HF) 교환 효과를 교환 연결에 통합하는 하이브리드 밀도 기능이 있습니다. 체계적인 정보 및 계산 결과는 특히 유기 화학 분야에 적합한 실험 데이터에 점점 더 가까워지고 있으며 화학 반응 메커니즘의 계산에서 큰 성공을 거두었습니다.
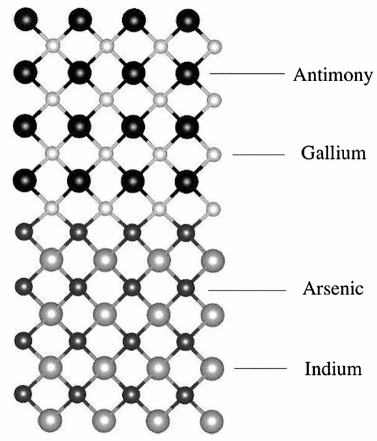
예를 들어, T. Garwood et al. 실험 값에 매우 가까운 PBE0 유형 하이브리드 화 [9]를 사용하여 InAs / GaSb II 유형 초 격자 구조 (그림 6에 표시된 모델)의 밴드 갭 데이터를 계산했으며 편차 범위는 약 3 %-11%입니다.
그림 6 VESTA를 사용하여 계산 한 하이브리드 DFT의 볼앤 스틱 InAs / GaSb SLS 모델
Kohn-Sham 단일 입자 에너지 스펙트럼을 기반으로 한 전자 밴드 구조 이론은 많은 물질을 정 성적으로 설명 할 수 있지만 정량적 관점에서는 만족스럽지 않습니다. 예를 들어, Si 및 GaAs와 같은 간단한 반도체 재료의 경우 LDA / GG에서 Kohn-Sham DFT가 제공하는 밴드 갭은 훨씬 작습니다. Ge 및 InN과 같은 소형 밴드 갭 반도체의 경우 LDA / GGA에서 얻은 금속은 금속입니다. 상태, 그러나 실험적인 관찰은 소위 LDA / GGA 밴드 갭 문제인 반도체입니다.
밴드갭 문제를 극복하기 위해 지역유효포텐셜에 기반한 Kohn-Sham 이론을 Non-Non-Sham 기반의 GKS(Generalized Kohn-Sham) 이론으로 확장하는 등 DFT의 이론적 틀에 많은 노력을 기울였다. 국소유효전위, 기타 잡종밀도함수이론, 단일체 그린의 함수에 기초한 다물체 섭동이론이 있다. 이 이론에서 Kohn-Sham DFT와의 교환 관련 잠재력은 교환 관련 자가 에너지 운영자에 해당합니다. 자가 에너지 연산자의 경우 비교적 간단하고 정확한 근사는 GW 근사(단일 입자 Green의 함수 G와 차폐된 쿨롱 효과 W의 곱)입니다. 특정 근사값에서 자체 에너지 연산자를 계산하여 해당 PES(IPS)를 얻을 수 있습니다. 여기 에너지의 준 입자. 이러한 새로운 개발 방향은 재료의 밴드 갭에 대한 설명을 개선했지만 대략적인 기능은 여전히 주관성이 크고 적용 범위가 상대적으로 제한적입니다. 아직까지 이론적 근거가 충분한 보편적인 DFT 방법은 없다. 재료의 전자 밴드 구조에 대한 정확한 설명 [10,11].
또한 기존 밀도 기능 이론을 기반으로하는 확장이 있습니다. 예를 들어, KS 궤도 에너지 차이에 기초한 시간-의존 밀도 함수 이론 (TDDFT)은 Schordinger 방정식을 단일 입자 Dirac 방정식으로 대체하는 데 사용됩니다. 밀도 밀도 기능 이론은 임의의 자기장 하에서 상호 작용하는 전자 시스템을 다루기 위해 강력한 상관 시스템의 LDA + U 및 CDFT (flow density 기능 이론)까지 확장됩니다.
참고 문헌
Xiang-Yuan Cui, Simon P. Ringer , 원자 프로브 현미경과 밀도 기능 이론 사이의 관계에서 [J] , 재료
특성화 (2018), https://doi.org/10.1016/ matchar.2018.05.015
B. Obot, DD Macdonald, ZM Gasem , 밀도 기능 이론
(DFT)는 새로운 유기 부식 방지제를 설계하기위한 강력한 도구입니다. 1 부 : 개요 [J] , Corrosion Science 99 (2015) 1–30
Geerlings, F. De Proft, W. Langenaeker, 개념적 밀도 기능 이론, 화학. 개정판 103 (2003) 1793–1873.
Nagy, 밀도 기능 이론 및 원자 및 분자에의 적용, Rev. 298 (1998) 1–79.
Koch, MC Holthausen, 밀도 기능 이론에 대한 화학자 안내서, Wiley-VCH, Weinheim, 2000.
Asad Mahmood, Fatih Tezcan, Gulfeza Kardas , 졸-겔 유래 Zn0.8Ga0.2O 전구체 겔의 열분해 : 동역학, 열역학 및 DFT 연구 [J] , Acta Materialia 146 (2018) 152-159
Parmod Kumar, Hitendra K. Malik, Anima Ghosh, R. Thangavel, K. Asokan , ZnO 및 N의 강자성 기원에 대한 통찰력
임플란트 ZnOthin 필름 : 실험 및 DFT 접근법 [J] , Journal of Alloys and Compounds 768 (2018) 323-328
Romaka, VV Romaka, N. Melnychenko, Yu. Stadnyk, L. Bohun, A. Horyn , VeCoeSb 3 원 시스템의 실험 및 DFT 연구 [J], 합금 및 화합물 저널 739 (2018) 771-779
Ibáñez, T. Woźniak, F. Dybala, R. Oliva, S. Hernández , R. Kudrawiec, 고압 라만 산란 벌크 HfS2 : 압축 하에서 층상 MS2 화합물 (M = Hf, Mo)에서 밀도 기능 이론 방법 비교 [J] , 과학 보고서 (2018) 8 : 12757, DOI : 10.1038 / s41598-018- 31051-y
Garwood, NA Modine, S. Krishna , 하이브리드 밀도 기능 이론을 이용한 InAs / GaSb 초 격자의 전자 구조 모델링 [J] , 적외 물리 및 기술 81 (2017) 27–31
Eugene S. Kryachko, Eduardo V. Ludena , 밀도 기능 이론 : 기초 검토 [J] , 물리 보고서 544 (2014) 123–239
B. Obot, DD Macdonald, ZM Gasem , DFT (Density Functional Theory)는 새로운 유기 부식 억제제 설계를위한 강력한 도구입니다. 1 부 : 개요 [J] , Corrosion Science 99 (2015) 1–30







