Pęknięcia zmęczeniowe są na ogół wynikiem okresowych odkształceń plastycznych w obszarach lokalnych. Zmęczenie definiuje się jako „awarię pod powtarzającym się obciążeniem lub innymi typami warunków obciążenia, a ten poziom obciążenia nie jest wystarczający do spowodowania uszkodzenia, gdy zostanie zastosowany tylko raz”. To odkształcenie plastyczne występuje nie z powodu teoretycznego naprężenia idealnego elementu, ale dlatego, że powierzchnia elementu nie może być faktycznie wykryta.
August Wöhler jest pionierem badań zmęczeniowych i przedstawia metodę empiryczną. W latach 1852-1870 wöhler badał postępującą awarię osi kolejowych. Zbudował stanowisko testowe pokazane na rysunku 1. Stanowisko to umożliwia jednoczesne obracanie i zginanie dwóch osi kolejowych. Wöhler wykreślił zależność między naprężeniem nominalnym a liczbą cykli prowadzących do uszkodzenia, co jest później znane jako wykres SN. Każda krzywa nadal nazywana jest linią awöhlera. Metoda Sn jest nadal najczęściej stosowaną metodą. Typowy przykład tej krzywej pokazano na rysunku 1.
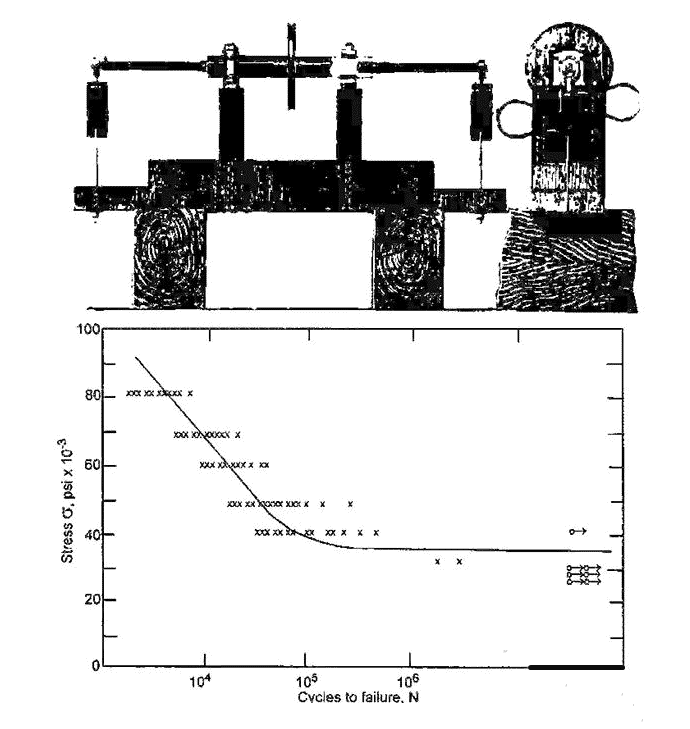
Na linii wöhlera można zaobserwować kilka efektów. Po pierwsze, zauważamy, że krzywa SN poniżej punktu przejścia (około 1000 cykli) jest nieprawidłowa, ponieważ naprężenie nominalne jest tutaj elastoplastyczne. Pokażemy później, że zmęczenie spowodowane jest uwolnieniem energii plastycznego odkształcenia ścinającego. Dlatego nie ma liniowej zależności między naprężeniem a odkształceniem przed pęknięciem i nie można go stosować. Pomiędzy punktem przejścia a granicą zmęczenia (około 107 cykli) analiza oparta na Sn jest ważna. Powyżej granicy zmęczenia nachylenie krzywej gwałtownie się zmniejsza, więc obszar ten jest często określany jako obszar „nieskończonej żywotności”. Ale tak nie jest. Na przykład, stop aluminium nie będzie miał nieskończonej żywotności, a nawet stal nie będzie miała nieskończonej żywotności przy obciążeniu o zmiennej amplitudzie.
Wraz z pojawieniem się nowoczesnej technologii wzmacniania, ludzie mogą bardziej szczegółowo badać pęknięcia zmęczeniowe. Obecnie wiemy, że powstawanie i propagację pęknięć zmęczeniowych można podzielić na dwa etapy. W początkowej fazie rysa propaguje się pod kątem około 45 stopni w stosunku do przyłożonego obciążenia (wzdłuż linii maksymalnego naprężenia ścinającego). Po przekroczeniu dwóch lub trzech granic ziaren, jego kierunek zmienia się i rozciąga się w kierunku około 90 stopni w stosunku do przyłożonego obciążenia. Te dwa etapy nazywane są pęknięciem etapu I i pęknięciem etapu II, jak pokazano na rysunku 2.
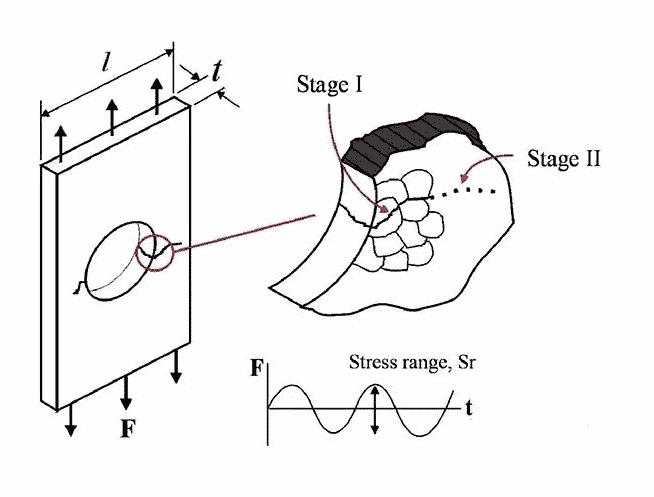
Jeśli obserwujemy pęknięcie stopnia I przy dużym powiększeniu, widzimy, że naprężenie przemienne doprowadzi do powstania ciągłego pasma poślizgu wzdłuż maksymalnej płaszczyzny ścinania. Te opaski poślizgowe przesuwają się tam iz powrotem, podobnie jak talia kart, co powoduje nierówne powierzchnie. Wklęsła powierzchnia ostatecznie tworzy „pączkujące” pęknięcie, jak pokazano na rysunku 3. W fazie I pęknięcie będzie się rozszerzać w tym trybie, aż napotka granicę ziaren i chwilowo się zatrzyma. Gdy do sąsiednich kryształów zostanie przyłożona wystarczająca ilość energii, proces będzie kontynuowany.
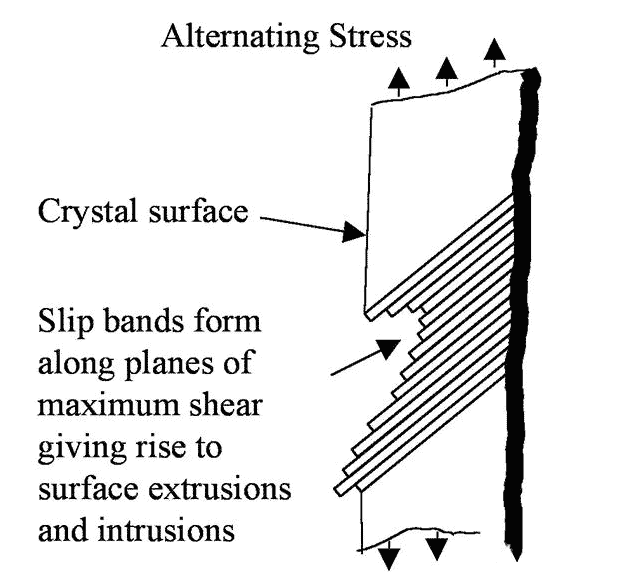
Po przekroczeniu dwóch lub trzech granic ziaren kierunek propagacji pęknięć wchodzi teraz w fazę II. Na tym etapie zmieniły się właściwości fizyczne propagacji pęknięć. Samo pęknięcie stanowi makroprzeszkodę dla przepływu naprężeń, powodując dużą koncentrację naprężeń plastycznych na wierzchołku pęknięcia. Jak pokazano na rysunku 4. Należy zauważyć, że nie wszystkie pęknięcia I stopnia rozwiną się do II stopnia.
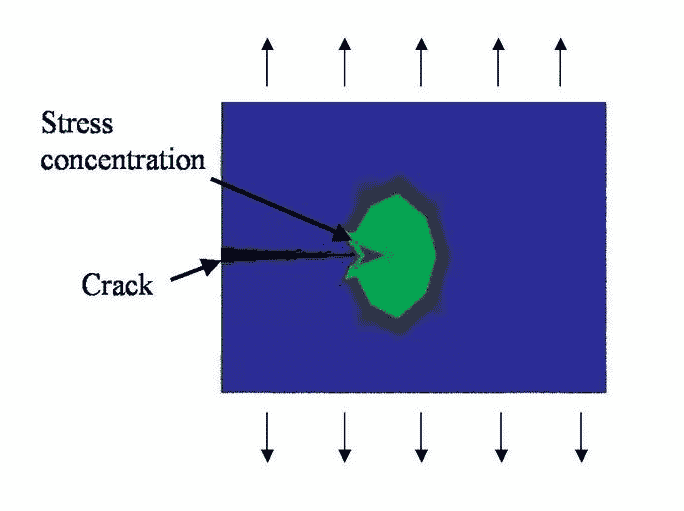
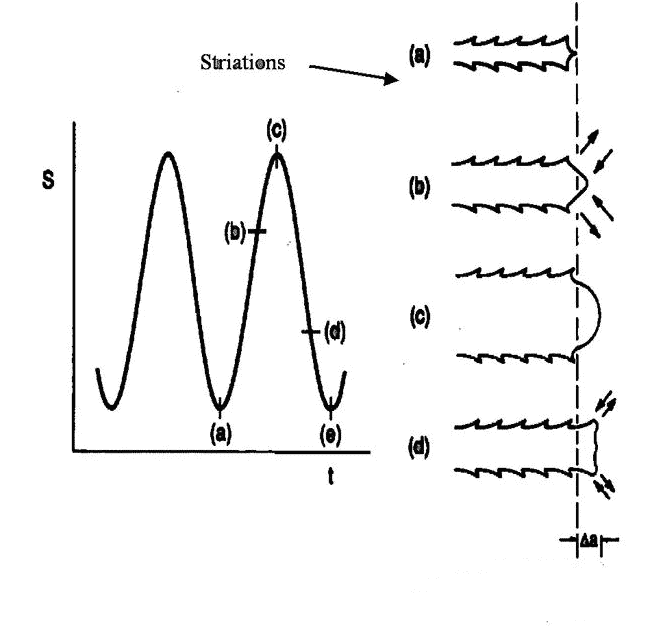
Aby zrozumieć mechanizm propagacji fazy II, musimy wziąć pod uwagę sytuację w przekroju wierzchołka pęknięcia podczas cyklu naprężeń. Jak pokazano na rysunku 5. Cykl zmęczeniowy rozpoczyna się, gdy naprężenie nominalne znajduje się w punkcie „a”. Gdy intensywność naprężeń wzrasta i przechodzi przez punkt „B”, zauważamy, że wierzchołek pęknięcia otwiera się, powodując lokalne plastyczne odkształcenie ścinające, a pęknięcie rozciąga się do punktu „C” w pierwotnym metalu. Gdy naprężenie rozciągające spada przez punkt „d”, obserwujemy, że wierzchołek pęknięcia zamyka się, ale trwałe odkształcenie plastyczne pozostawia unikalne ząbkowanie, tzw. „linię cięcia”. Kiedy cały cykl kończy się w punkcie „e”, obserwujemy, że pęknięcie zwiększyło teraz długość „Da” i utworzyło dodatkowe linie przekroju. Obecnie rozumie się, że zakres wzrostu pęknięcia jest proporcjonalny do zakresu zastosowanego odkształcenia sprężysto-plastycznego wierzchołka pęknięcia. Większy zakres cykli może tworzyć większe Da.
Czynniki wpływające na tempo wzrostu pęknięć zmęczeniowych
Zbadano i wyjaśniono koncepcyjnie wpływ następujących parametrów na szybkość rozwoju pęknięć zmęczeniowych:
1Naprężenie ścinające
Z wykresu widać, że pewna „ilość” naprężenia ścinającego jest uwalniana podczas okresowej zmiany siły naprężenia nominalnego. A im większy zakres zmian stresu, tym większa uwalniana energia. Na podstawie krzywej SN pokazanej na rysunku 1 widać, że trwałość zmęczeniowa maleje wykładniczo wraz ze wzrostem zakresu cyklu naprężeń.
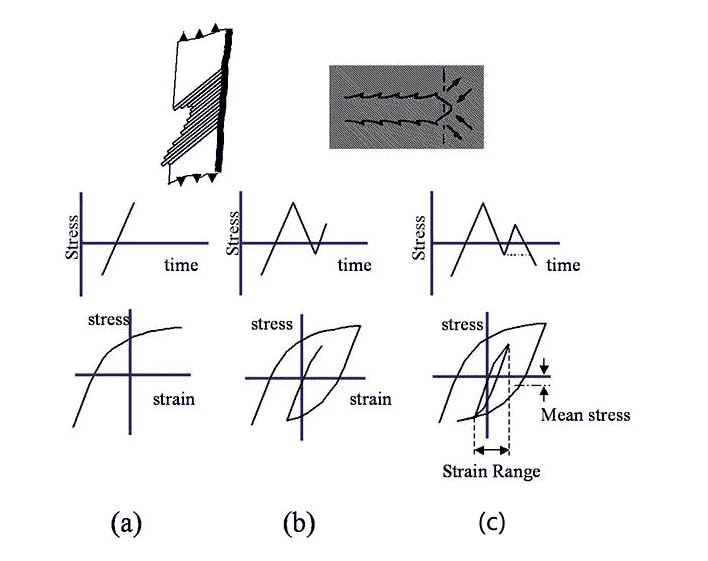
2 średni stres
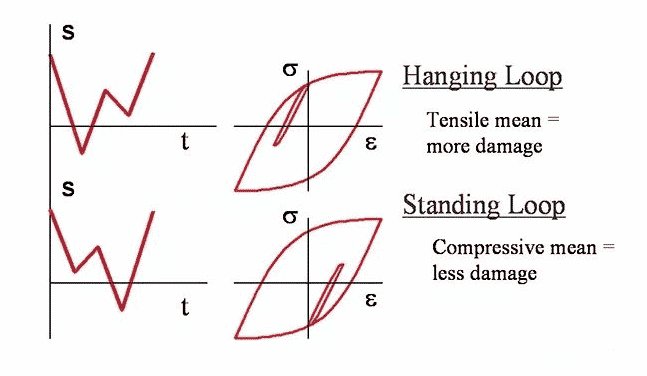
Naprężenie średnie (naprężenie szczątkowe) jest również czynnikiem wpływającym na wskaźnik zmęczenia. Koncepcyjnie, jeśli naprężenie rozszerzające zostanie przyłożone do pęknięcia fazy II, pęknięcie zostanie zmuszone do otwarcia, więc każdy cykl naprężeń będzie miał bardziej znaczący wpływ. Wręcz przeciwnie, jeśli zastosuje się średnie naprężenie ściskające, pęknięcie zostanie zmuszone do zamknięcia, a każdy cykl naprężeń musi przezwyciężyć naprężenie przed ściskaniem, zanim pęknięcie będzie mogło dalej się rozszerzać. Podobne koncepcje dotyczą również pęknięć I stopnia.
3 wykończenie powierzchni
Ponieważ pęknięcia zmęczeniowe zwykle pojawiają się najpierw na powierzchni elementów, na których występują defekty, jakość powierzchni poważnie wpłynie na prawdopodobieństwo wystąpienia pęknięć. Chociaż większość próbek testowych materiałów ma lustrzane wykończenie, dzięki czemu osiągną również najlepszą trwałość zmęczeniową. W rzeczywistości większości komponentów nie można porównać z próbkami, dlatego musimy zmodyfikować właściwości zmęczeniowe. Wykończenie powierzchni ma większy wpływ na zmęczenie elementów poddanych cyklom naprężeń o niskiej amplitudzie.
4 obróbka powierzchni
Obróbkę powierzchni można zastosować w celu zwiększenia wytrzymałości zmęczeniowej komponentów. Celem obróbki powierzchni jest wytworzenie szczątkowego naprężenia ściskającego na powierzchni. W okresie niskiej amplitudy naprężenie na powierzchni jest oczywiście niskie, a nawet utrzymuje stan ściskania. Dzięki temu żywotność zmęczeniowa może zostać znacznie przedłużona. Jednak, jak wskazaliśmy, sytuacja ta dotyczy tylko elementów poddanych cyklom naprężeń o niskiej amplitudzie. Jeżeli zastosowany zostanie okres o wysokiej amplitudzie, kompresja wstępna zostanie pokonana przez okres o wysokiej amplitudzie, a jej zalety zostaną utracone. Podobnie jak w przypadku jakości powierzchni, wpływ obróbki powierzchni można wykazać za pomocą modelowania.







