Teoria gęstości funkcjonalnej (DFT) jest szeroko stosowana w dziedzinie fizyki materii skondensowanej, nauki o materiałach, chemii kwantowej i nauk przyrodniczych jako metoda przybliżenia w układach wielocząsteczkowych. Na przykład ryc. 1 (c) to 72-atomowa struktura superkomórkowa obliczona metodą DFT [1]. Metoda symulacji obliczeniowej opartej na technologii DFT może nie tylko badać istniejące materiały, ale także przewidywać nowe materiały.
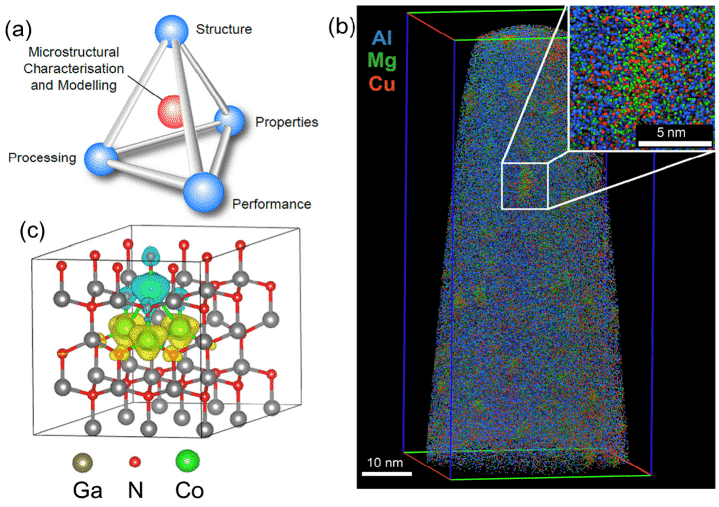
rysunek 1 (a) Potencjalny związek między charakterystyką mikroskopową, strukturą, przetwarzaniem, właściwościami i właściwościami, (b) Dane APT dla stopów Al-Cu-Mg zawierających około 20 milionów atomów, (c) 72 atom dla obliczeń DFT Przykład superkomórki
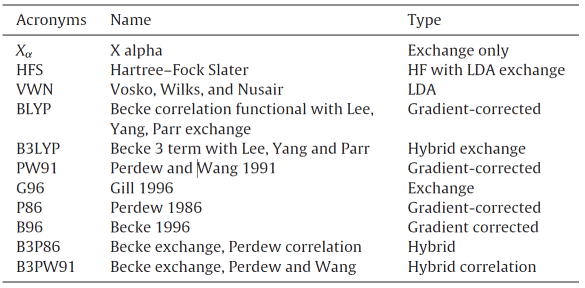
Funkcjonalny to mapowanie z przestrzeni wektorowej na skalarną, funkcja funkcji. W tabeli 1 wymieniono niektóre z zaproponowanych rodzajów funkcjonałów gęstości, niektóre z nich pochodzą z podstawowej mechaniki kwantowej, a niektóre z funkcji parametrycznych, z których każda ma swoje zalety i wady oraz zakres zastosowania [2]. Istotą metody DFT jest wykorzystanie gęstości elektronowej jako nośnika wszystkich informacji w molekularnym (atomowym) stanie podstawowym, a nie funkcji falowej pojedynczego elektronu, aby układ wieloelektronowy mógł zostać przekształcony w problem pojedynczego elektronu. Zakładając, że liczba elektronów wynosi N, liczba zmiennych w funkcji falowej wynosi 3N, a teoria funkcjonalna gęstości zmniejsza liczbę zmiennych do trzech zmiennych przestrzennych, co upraszcza proces obliczania i zapewnia dokładność obliczeń.
Tabela 1 Niektóre typy funkcjonalne o przybliżonej gęstości
Rozwój teorii funkcjonalnej gęstości można z grubsza podzielić na trzy etapy. Pierwszy etap miał miejsce w 1927 r. Thomas i Fermi zaproponowali model Thomasa-Fermiego oparty na idei elektronicznej hipotezy gazowej w idealnych warunkach. Po raz pierwszy wprowadzono koncepcję teorii funkcjonalnej gęstości, która stała się prototypem późniejszej metody DFT.
Punktem wyjścia modelu Thomasa-Fermiego jest założenie, że nie ma interakcji między elektronami i nie występuje interferencja zewnętrzna, wówczas równanie Schrödingera dla ruchu elektronu można wyrazić jako:
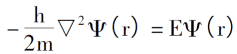
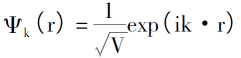
Wprowadzając zasadę rozmieszczenia elektronów poniżej 0K, gęstość elektronów, całkowitą energię pojedynczych elektronów i gęstość energii kinetycznej układu to:
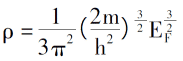
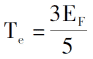
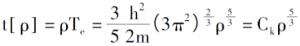
Wprowadzając opis potencjału kulombowego i pola zewnętrznego między elektronami, można uzyskać całkowitą ekspresję energii układu elektronicznego określoną jedynie przez funkcję gęstości elektronowej [3].
Chociaż model upraszcza formę obliczeniową i proces, nie uwzględnia interakcji między elektronami. Nie opisuje dokładnie elementów energii kinetycznej, dlatego nie ma zastosowania w wielu systemach. Jednak zainspirowani tą nowatorską ideą badawczą, po wielu latach wysiłków, właściwi badacze zasadniczo udoskonalili treść teorii funkcjonalnej gęstości i ostatecznie opracowali ścisłą teorię funkcjonalną.
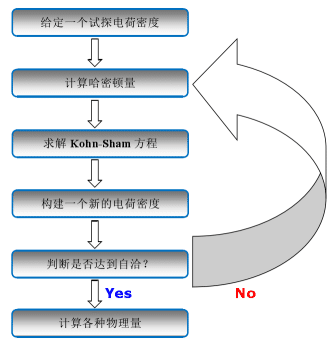
Ryc. 2 Schemat ideowego spójnego procesu iteracyjnego opartego na DFT
Twierdzenie Hohenberga-Kohna i równanie Kohna-Shama odegrały kluczową rolę w tworzeniu i doskonaleniu metody DFT i zostały okrzyknięte dwoma kamieniami węgielnymi DFT.
(1) Twierdzenie Hohenberga-Kohna
Podstawową ideą twierdzenia Hohenberga-Kohna jest to, że wszystkie wielkości fizyczne w układzie mogą być jednoznacznie określone przez zmienne zawierające tylko gęstość elektronów, a metodą realizacji jest uzyskanie stanu podstawowego układu za pomocą zasady wariacyjnej. Teoria ta dotyczy głównie niejednorodnego modelu gazu elektronowego i składa się z dwóch pod-twierdzeń. i) układ elektronowy, który ignoruje spin przy potencjale zewnętrznym (potencjał inny niż interakcja elektronowa), którego potencjał zewnętrzny można jednoznacznie określić za pomocą gęstości elektronowej; ii) dla danego potencjału zewnętrznego energia stanu podstawowego systemu stanowi minimum wartości funkcjonalnej energii. Funkcjonalność energetyczną systemu można zatem opisać jako:
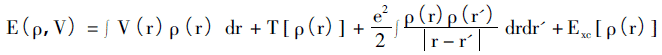
Prawa strona równania to energia potencjalna, pojęcie energii kinetycznej, oddziaływanie kulombowe między elektronami i związana z wymianą energia potencjalna w polu zewnętrznym.
Twierdzenie to nie podaje specyficznych wyrażeń funkcji gęstości elektronowej, funkcji energii kinetycznej i funkcji związanej z wymianą, więc konkretne rozwiązanie wciąż nie jest możliwe.
(2) Równanie Kohna-Shama
Do 1965 r. Kohn i Shen Lujiu ustalili równanie Kohna-Shama, podając szczegółowy opis każdego elementu, a teoria funkcjonalna gęstości zaczęła wchodzić w praktyczny etap stosowania. Zaproponowali, aby funkcjonałowie energii kinetycznej wykorzystali funkcjonały energii kinetycznej cząstek bez interakcji w celu przybliżenia podstawienia, a różnice między nimi są uwzględnione w niewiadomych funkcjonałów związanych z wymianą [4]. Zmianę ρ zastępuje się przez odmiana Φi (r), a mnożnik Lagrange'a zostaje zastąpiony przez Ei. Równanie pojedynczego elektronu jest następujące:
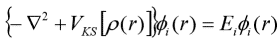
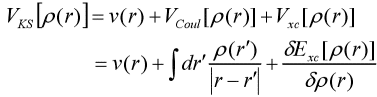
Powyżej jest równanie Kohna-Shama.
Równanie Kohna-Shama daje wyraźne wyrażenie wszystkiego poza funkcjami związanymi z wymianą, a także kategoryzuje złożone efekty do tego terminu. W tym momencie trudność obliczeniowa jest znacznie uproszczona, a cała praca rozpoczyna się od opisania rozszerzenia funkcjonalnego związanego z wymianą. Jednocześnie przybliżona postać potencjału związanego z wymianą również bezpośrednio określa dokładność teorii funkcjonalnej gęstości.
Lokalną gęstość aproksymacji (LDA) zaproponowali również Kohn i Shen Lujiu w 1965 r. Celem jest przybliżenie nieznanych powiązań wymiany, tak aby metodę DFT można było zastosować do rzeczywistych obliczeń. LDA wykorzystuje funkcję gęstości jednorodnego gazu elektronowego do obliczenia relacji wymiany nierównomiernego gazu elektronowego. Zakładając, że gęstość elektronów w układzie zmienia się bardzo niewiele z przestrzenią, relację wymiany niejednorodnego gazu elektronowego można wyrazić jako:
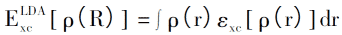
Odpowiedni potencjał korelacji wymiany można wyrazić jako:
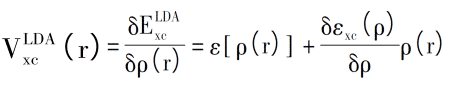
Na przykład Asad Mahmood i in. wykorzystał VASP do porównania równowagowych parametrów strukturalnych obliczeń LDA-PBE i GGA-PAW, a także zbadał wpływ domieszkowania Ga na hybrydyzację orbitalną elektronów, a także właściwości optyczne i geometrię kryształu, z rysunku 3 (c). Można zauważyć, że orbitale Ga-2s i Ga-2p znacząco przyczyniają się do przewodzenia, niższe VB również przyczynia się do Ga-2p, a pasmo zanieczyszczeń na dole CB sugeruje dodatkową barierę energetyczną, elektron między VB i CB. Przejście musi przekroczyć barierę energetyczną [5].
Rycina 3 Wyniki obliczeń
(a) Zoptymalizowana superkomórka ZnO domieszkowana 3x3x3 Ga, (b) struktura pasmowa, (c) gęstość DOS
Aby dokładniej obliczyć rzeczywisty system materiałowy, w 1986 r. Becke, Perdew i Wang i in. zaproponowano uogólnioną aproksymację gradientu (GGA), która jest najczęściej stosowaną metodą przetwarzania w obliczeniach funkcjonalnych gęstości.
Metodą przetwarzania GGA jest przepisanie oryginalnej reprezentacji do postaci funkcjonalnej zawierającej funkcje gęstości elektronowej i gradientu, a także opis spinu, a wynikowa funkcja związana z wymianą jest następująca:
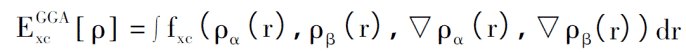
W GGA potencjał korelacji wymiany można również rozłożyć na energię wymiany i energię korelacji. Jak więc skonstruować rozsądne wyrażenie dla tych dwóch części? Beckc i in. wierzy, że konkretna forma funkcjonalna może być z zasady konstruowana arbitralnie i nie musi uwzględniać rzeczywistego znaczenia fizycznego, jak np. GGA-PW91; natomiast Perdew i in. zwolennicy powrotu do czystej teorii obliczeń mechaniki kwantowej w miarę możliwości, wszystkie wielkości fizyczne są tylko obliczane. Wychodząc od podstawowych stałych, takich jak elektronowa masa statyczna, stała Plancka i prędkość światła, wyrażenia funkcjonalne nie powinny zawierać nadmiernych parametrów empirycznych, takich jak GGA-PBE (Perdew-Burke-Enzerhoff), który jest często używany w dziedzinach takich jak materia skondensowana fizyka.
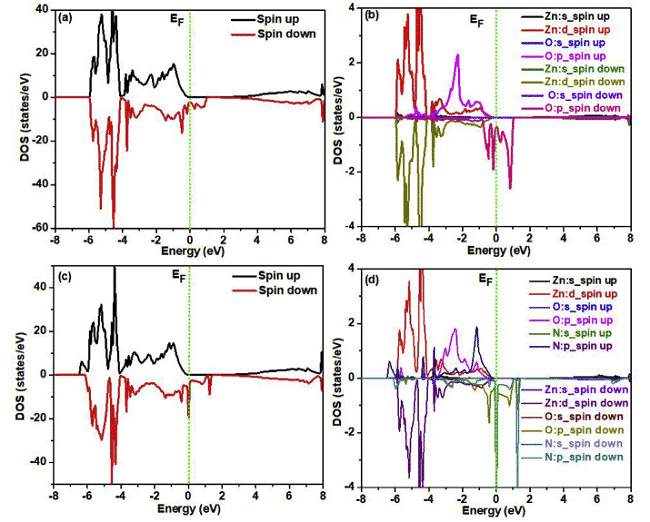
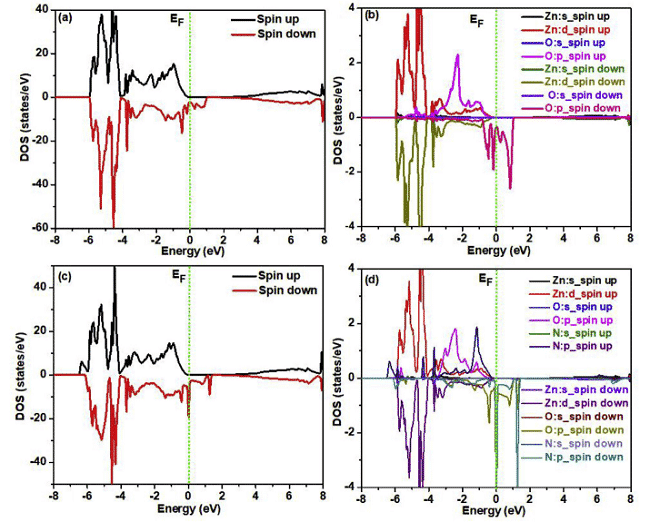
Ostatnio Parmod Kumar i L. Romaka i in. przeprowadził powiązane badania z wykorzystaniem FP-LAPW (fali o pełnym potencjale liniowo wzmocnionej fali płaskiej) odpowiednio w WIEN2k i Elk v2.3.22, w których potencjał korelacji wymiany ma postać GGA-PBE, ryc. 4, 5 Obliczone wyniki dla odpowiednich gęstość stanów i rozkład gęstości ładunku [6,7].
Ryc. 4 Całkowita gęstość stanów i lokalna gęstość stanów superkomórek spolaryzowanych spinowo ZnO bez iniekcji i implantacji azotu
Ryc. 5 Rozkład funkcji lokalizacji elektronów (Y) i gęstości ładunku (r) w tellurku VCoSb J. Ibáñez, T. Woźniak i in. przetestowano poprawność teorii funkcjonalnej o różnej gęstości, aby przewidzieć dynamikę sieci HfS2 pod ciśnieniem.
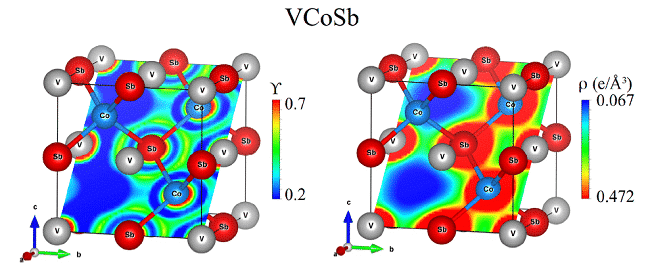
Tabela obserwacyjna 2 wykazała, że GGA-DFT prawidłowo opisuje dynamikę sieci wysokiego ciśnienia HfS2, biorąc pod uwagę interakcję vdW, podczas gdy obliczenia LDA-DFT są szeroko stosowane do przewidywania struktury i charakterystyk drgań związków 2D w warunkach środowiskowych i nie można ich odtworzyć podczas kompresji warunki. Zachowanie HfS2, które wskazuje, że użycie DFT-LDA do obliczenia ściśliwości TMDC i parametrów Grüneisen spowoduje duże błędy [8].
Tabela 2 Częstotliwość Ramana (ωi0), współczynnik ciśnienia (ai0) i parametr Grüneisen (γi)
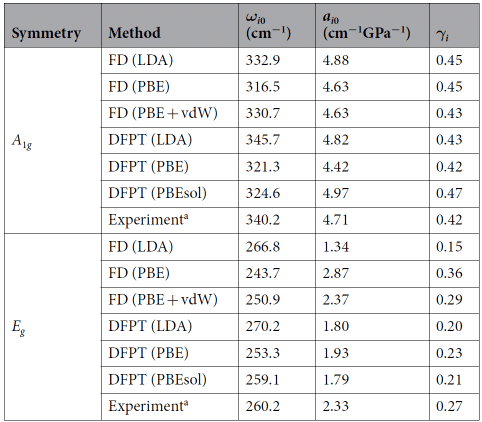
Oprócz algorytmów LDA i GGA istnieją również hybrydowe funkcjonały gęstości, które wykorzystują efekty wymiany Hatree-Focka (HF) w skojarzeniach wymiany w sposób hybrydowy, takie jak B3LYP, który był popularny w 1998 roku. Teorie te zawierają coraz więcej systematyczne informacje, a wyniki obliczeń zbliżają się coraz bardziej do danych eksperymentalnych, szczególnie odpowiednich w dziedzinie chemii organicznej, i osiągnęły wielki sukces w obliczaniu mechanizmu reakcji chemicznej.
Na przykład T. Garwood i in. obliczył dane pasma wzbronionego struktury nadbudowy typu InAs / GaSb II (model pokazany na ryc. 6) przy użyciu hybrydyzacji typu PBE0 [9], co jest bardzo zbliżone do wartości eksperymentalnej, a zakres odchyleń wynosi około 3 %-11%.
Rycina 6 Model InAs / GaSb SLS typu hybrydowego DFT obliczony za pomocą VESTA
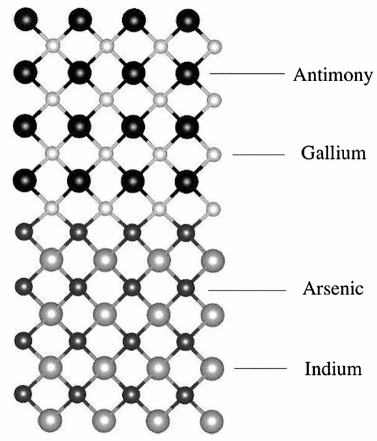
Teoria struktury pasm elektronowych oparta na widmie energii pojedynczych cząstek Kohna-Shama może jakościowo opisać wiele materiałów, ale nie jest zadowalająca z ilościowego punktu widzenia. Na przykład w przypadku prostych materiałów półprzewodnikowych, takich jak Si i GaAs, pasmo wzbronione podane przez Kohn-Sham DFT pod LDA / GG jest znacznie mniejsze; w przypadku półprzewodników o małych odstępach, takich jak Ge i InN, metal otrzymany z LDA / GGA to metal. Stan, ale obserwacją eksperymentalną jest półprzewodnik, który jest tak zwanym problemem przerwy pasmowej LDA / GGA.
Aby przezwyciężyć problem pasma wzbronionego, ludzie podjęli wiele wysiłków w zakresie teoretycznych ram DFT, takich jak rozszerzenie teorii Kohna-Shama opartej na lokalnym potencjale efektywnym na uogólnioną teorię Kohna-Shama (GKS) opartą na lokalny efektywny potencjał i Inna hybrydowa teoria funkcjonału gęstości, istnieje wielociałowa teoria perturbacji oparta na funkcji jednociałowego Greena. W tej teorii potencjał związany z wymianą z DFT Kohna-Shama odpowiada operatorowi energii własnej związanej z wymianą. Dla operatora energii własnej stosunkowo prostym i dokładnym przybliżeniem jest przybliżenie GW (iloczyn funkcji Greena dla pojedynczej cząstki G i ekranowanego efektu Coulomba W). Obliczając operator energii własnej z pewnym przybliżeniem, możemy uzyskać odpowiedni PES (IPS). Quasi-cząstki w energii wzbudzenia. Chociaż te nowe kierunki rozwoju poprawiły opis pasma wzbronionego materiałów, przybliżone funkcjonalności nadal mają dużą subiektywność, a zakres zastosowania jest stosunkowo ograniczony. Jak dotąd nie ma uniwersalnej metody DFT o wystarczającej podstawie teoretycznej. Dokładny opis struktury elektronowej pasmowej materiału [10,11].
Ponadto istnieją pewne rozszerzenia oparte na istniejącej teorii funkcjonalnej gęstości. Na przykład teoria funkcjonalna gęstości zależna od czasu (TDDFT) oparta na różnicy energii orbitalnej KS jest używana do zastąpienia równania Schordingera równaniem Diraca dla pojedynczych cząstek. Teoria funkcjonalna gęstości gęstości rozciąga się na LDA + U silnych układów korelacji i teoria funkcjonalna gęstości przepływu (CDFT) do radzenia sobie z oddziaływującymi układami elektronowymi w dowolnych polach magnetycznych.
Bibliografia
Xiang-Yuan Cui, Simon P. Ringer, O związku między mikroskopem sondy atomowej a symulacjami funkcjonalnymi teorii gęstości [J], Materiały
Charakterystyka (2018), https://doi.org/10.1016/ matchar.2018.05.015
B. Obot, DD Macdonald, ZM Gasem, Teoria funkcjonalna gęstości
(DFT) jako potężne narzędzie do projektowania nowych organicznych inhibitorów korozji. Część 1: Przegląd [J], Corrosion Science 99 (2015) 1–30
Geerlings, F. De Proft, W. Langenaeker, Teoria funkcjonalnych gęstości koncepcyjnych, Chem. Rev. 103 (2003) 1793–1873.
Nagy, Teoria funkcjonalna gęstości i zastosowanie do atomów i cząsteczek, Rev. 298 (1998) 1–79.
Koch, MC Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2000.
Asad Mahmood, Fatih Tezcan, Gulfeza Kardas, Termiczny rozkład żelu prekursorowego Zn0.8Ga0.2O pochodzącego z zolu: badania akinetyczne, termodynamiczne i DFT [J], Acta Materialia 146 (2018) 152-159
Parmod Kumar, Hitendra K. Malik, Anima Ghosh, R. Thangavel, K. Asokan, Wgląd w pochodzenie ferromagnetyzmu w ZnO i N
wszczepione filmy ZnOthin: eksperymentalne i podejście DFT [J], Journal of Alloys and Compounds 768 (2018) 323-328
Romaka, VV Romaka, N. Melnychenko, Yu. Stadnyk, L. Bohun, A. Horyn, Eksperymentalne i DFT badanie układu trójskładnikowego VeCoeSb [J], Journal of Alloys and Compounds 739 (2018) 771-779
Ibáñez, T. Woźniak, F. Dybala, R. Oliva, S. Hernández, R. Kudrawiec, Wysokociśnieniowe rozpraszanie Ramana w parze HfS2: porównanie metod teorii funkcjonalnej gęstości w warstwowych związkach MS2 (M = Hf, Mo) pod kompresją [J], Raporty naukowe (2018) 8: 12757, DOI: 10.1038 / s41598-018- 31051-y
Garwood, NA Modine, S. Krishna, Elektroniczne modelowanie struktury superklat InAs / GaSb z teorią funkcjonalną hybrydowej gęstości [J], Infrared Physics & Technology 81 (2017) 27–31
Eugene S. Kryachko, Eduardo V. Ludena, Teoria funkcjonalna gęstości: recenzja podstaw [J], Physics Reports 544 (2014) 123–239
B. Obot, DD Macdonald, ZM Gasem, Gęstość funkcjonalna teoria (DFT) jako potężne narzędzie do projektowania nowych organicznych inhibitorów korozji. Część 1: Przegląd [J], Corrosion Science 99 (2015) 1–30








