Wskazówki: Podstawowe zasady i zastosowania dynamiki molekularnej

Aby mikroskopowy system symulacji odzwierciedlał makroskopowe zjawiska eksperymentalne, konieczne jest okresowe replikowanie symulowanego układu obiektów poprzez okresowe warunki brzegowe, aby uniknąć efektów krawędziowych, które nie występują w praktyce. W zasadzie teoretyczne badanie dowolnego układu molekularnego wymaga rozwiązania zależnego od czasu równania Schrödingera. Jednak w praktyce większą uwagę zwraca się na trajektorię jądra. Trajektorię taką można otrzymać rozwiązując klasyczne mechaniczne równanie ruchu z wykorzystaniem przybliżenia Borna-Oppenheimera. Alder i Wainwright stwierdzili, że eksperymenty symulacyjne komputerowe staną się ważnym pomostem łączącym makroskopowe zjawiska eksperymentalne z mikroskopijną naturą. Po 10 latach pierwszych eksperymentów symulacyjnych dynamiki molekularnej francuski fizyk Verlet zaproponował algorytm całkujący równania ruchu Newtona. Jednocześnie zaproponowano inny zestaw algorytmów generowania i rejestracji par sąsiadujących atomów, co znacznie upraszcza obliczenia interakcji między atomami. Te dwa algorytmy są nadal szeroko stosowane w praktyce w niektórych wariantach [1, 2].

W ciągu ostatnich kilku dziesięcioleci opracowano różnorodne metody symulacji na poziomie atomowym, w tym statykę sieci, dynamikę sieci, metodę Monte Carlo i dynamikę molekularną. Wśród nich dynamika molekularna jest szczególnie odpowiednia do badania odkształceń plastycznych. Bada zachowanie procesu deformacji w czasie rzeczywistym poprzez rozwiązanie równania Newtona układu oddziaływań atomowych niektórych określonych funkcji potencjalnych oddziaływań międzyatomowych i uwzględnia brak uproszczenia sieci. Harmonijność, nierównomierność wysokości naprężeń wewnętrznych i przejściowa reakcja układu.

Dynamika molekularna polega głównie na mechanice newtonowskiej w celu symulacji ruchu układu molekularnego w celu wydobycia próbek z układów złożonych z różnych stanów układu molekularnego, a tym samym obliczenia całki konfiguracji układu i dalszego obliczenia układu na podstawie wyników konfiguracji całka. Wielkości termodynamiczne i inne właściwości makroskopowe. Rozwiązuje równanie ruchu dla układu wieloobiektowego złożonego z jąder i elektronów. Jest to metoda obliczeniowa, która może rozwiązać problem dynamiki systemu wielu kompozycji atomowych. Może nie tylko bezpośrednio symulować makroskopowe cechy ewolucji substancji, ale także zgadzać się z wynikami badań. Podobne obliczenia mogą również zapewnić wyraźny obraz mikrostruktury, ruchu cząstek i ich związku z właściwościami makroskopowymi, zapewniając potężne wsparcie techniczne dla rozwoju nowych teorii i koncepcji.

Przedmiotem dynamiki molekularnej jest układ cząsteczkowy. Interakcja między atomami w układzie opisana jest funkcją potencjalną. Dlatego prawidłowy wybór rodzaju funkcji potencjalnej i jej parametrów odgrywa ważną rolę w wynikach symulacji. W większości przypadków funkcja energii potencjalnej upraszcza opis deformacji geometrycznej cząsteczki do tego stopnia, że stosuje się tylko prosty składnik harmoniczny i funkcję trygonometryczną; zamiast interakcji między atomami wiążącymi, używana jest tylko interakcja Coulomba i potencjał Lennarda-Jonesa. Połączone, aby opisać. Wśród nich opis siły oddziaływania między atomami jest zwykle empiryczny lub półempiryczny, co może poprawić wydajność obliczeniową, ale nie może w pełni ujawnić właściwości wielu wiązań elektronowych, szczególnie złożoności związanej z jego strukturą i chemią w sąsiedztwo wad. Samozgodna funkcja wariacyjna. Funkcja potencjału EAM (Embedded-atom model) Daw i Baskws łączy w pewnym stopniu właściwości wielu ciał wiązań elektronicznych.

Wiarygodność funkcji potencjalnej zależy głównie od dokładności parametrów pola siły, a parametry pola siły można uzyskać przez dopasowanie eksperymentalnych danych obserwacyjnych i kwantowo mechanicznych danych ab initio. Obecnie najczęściej stosowanym polem siły molekularnej w symulacji biologicznych układów makrocząsteczkowych jest pole siły CHARMM i pole siły AMBER, które jest polem siły molekularnej do wczesnych badań makrocząsteczek biologicznych. Istniejące parametry pola siłowego są ciągle optymalizowane, a typy objętych nimi cząsteczek również się rozszerzają. Model gruboziarnisty zyskuje coraz więcej uwagi w obliczeniowych badaniach biofizycznych, ponieważ gruboziarniste cząstki są zdefiniowane w tym modelu, odpowiadając kilku atomom lub grupom atomowym, a nawet cząsteczkom w modelu wszystkich atomów. Liczba cząstek w układzie jest zmniejszona, dzięki czemu można znacznie poprawić skalę czasową i przestrzenną symulacji, ale szczegóły atomowe również zostaną utracone. Symulacje dynamiki molekularnej oparte na tym modelu są odpowiednie do badania powolnych zjawisk biologicznych lub zjawisk biologicznych zależnych od dużych zespołów.

Podstawową zasadą projektowania podstawowego pola siły jest minimalizacja narzutu energii obliczeniowej w kroku czasu w celu maksymalizacji skali symulacji. Jest to szczególnie ważne w przypadku pełnego pola sił atomowych, nawet w przypadku tak zwanego modelu gruboziarnistego. W szczególności zasada ta jest niezwykle ważna, jeśli chcesz symulować skale czasu w mikrosekundach, a nawet milisekundach.

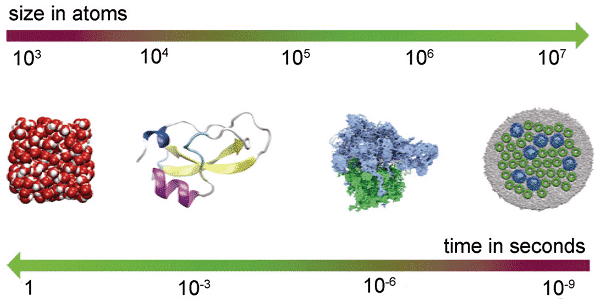
Rycina 1 pokazuje odwrotną zależność między czasem i przestrzenią wymiarów dynamiki molekularnej, od lewej do prawej na rysunku: (1) woda, podstawowe składniki komórek; (2) bydlęcy inhibitor trypsyny, enzym, którego „Zachowanie oddechowe można badać w skali milisekundowej; (3) rybosomy, złożone urządzenie biologiczne, które może dekodować informacje genetyczne i wytwarzać białka; (4) fioletowe bakteryjne fragmenty błony fotosyntetycznej, z 25 milionami atomów, rysunek pokazuje kompleks gromadzący światło osadzony w dwuwarstwie fosfolipidowej i centrum reakcji fotochemicznej.

Rycina 1 Skala zależności między czasem i przestrzenią klasycznej dynamiki molekularnej

Wraz z szybkim rozwojem procesorów komputerowych i rozwojem masowo równoległych architektur obliczeniowych, połączeniem masowo zrównoleglonych lub zastrzeżonych technik architektury ze skalowalnymi programami dynamiki molekularnej, symulacje komputerowe wahają się od przemieszczeń do mechanizmów deformacji opartych na granicach ziarna. Cały zakres wielkości ziaren otwiera nowe możliwości eksploracji granic badawczych systemów materiałowych.

Na przykład William Gonçalves i in. wykorzystał funkcję potencjalną Wolf BKS (van Beest, Kramer i van Santen) do opisania interakcji między atomami, używając wielkoskalowego symulatora równoległości atomowej / molekularnej LAMMPS (Large-Atomic / Molecular Massively Parallel). Symulator) badał dynamikę molekularną elastyczności i wytrzymałości aerożeli krzemionkowych. Wykorzystali algorytm prędkości-Verleta i krok czasowy 1,0 fs oraz zastosowali okresowe warunki brzegowe we wszystkich trzech kierunkach.

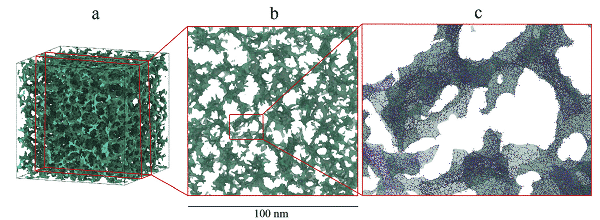
Ryc. 2 to schemat 3D symulowanej próbki o dużej objętości ponad 7 000 000 atomów, sekcja próbki o grubości 20 nm i częściowy powiększony widok (niebieski to atom tlenu, czerwony to atom krzemu) oraz rysunek 3 (a ) to aerożel 803 nm 3. Próbkę poddano jednoosiowemu testowi rozciągania w celu uzyskania krzywej naprężenie-odkształcenie wynoszącej 300 K, (bd) jest typowym obrazem pękania ciągliwego i (e) logarytmiczną zależnością między wytrzymałością na rozciąganie a objętością próbki. Przeanalizowali, że w celu zapewnienia właściwej oceny właściwości mechanicznych, takich jak elastyczność, wielkość symulowanej próbki jest co najmniej 8 razy większa od wielkości porów, podczas gdy aerożel krzemionkowy o dodatniej wysokości powierzchni wymaga stosunkowo niskiej prędkości odkształcania, aby zapewnić quasi- warunki statyczne.

Ryc. 2 Symulowana próbka aerożelu krzemionkowego (ponad siedem milionów atomów)

Ryc. 3 Krzywa naprężenie-odkształcenie (a), zależność siła-objętość (e) i obraz złamania (bd) jednoosiowego testu na rozciąganie

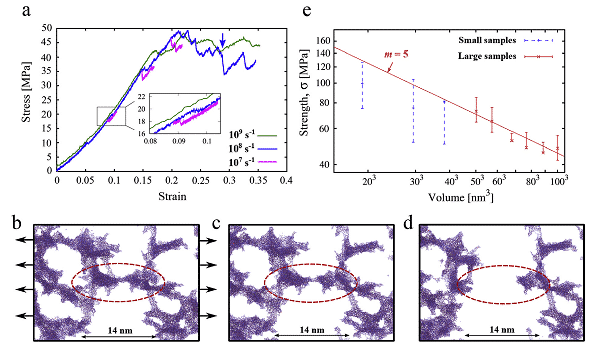
Zasadniczo krytyczny rozmiar ziarna dc wynosi około 20-30 nm, a większe odkształcenie dla rozmiaru ziarna (50-100 nm) jest determinowane głównie przez przemieszczenia; gdy rozmiar ziaren jest mniejszy niż 30 nm, jest on głównie zdominowany przez proces deformacji GB, a wielkość ziaren jest zmniejszona. Powoduje to zmniejszenie siły i stresu płynięcia, tj. „Efekt przeciw Halla-Petcha”. Jednak obszerne porównanie potencjałów wielu ciał i par używanych do modelowania GB w metalach fcc i bcc ujawnia, że istnieje niewielka różnica jakościowa w zachowaniu przewidywanym przez te różne opisy sił, co sugeruje, że efekty wielu ciał mogą nie dominować w zachowaniu GB.

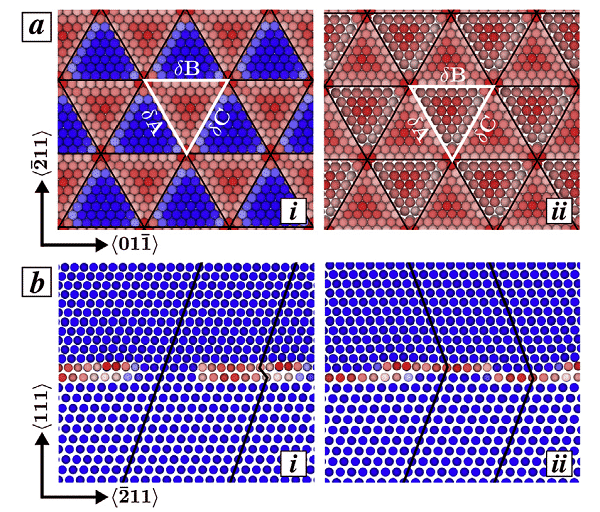
Bejaud, J. Durinck i in. wykorzystano symulację dynamiki molekularnej do badania interakcji między zdeformowanymi bliźniakami i nanostrukturalnymi interfejsami Cu / Ag, a także przeanalizowano wpływ struktury interfejsu na zarodkowanie, ekspansję i pogrubienie bliźniaków oraz wyjaśniono interfejs niedopasowania. Rola siatki przemieszczeń. Ryc. 4 pokazuje siatkę częściowego przemieszczenia Shockleya (podświetloną czarnymi liniami), trójkątny wzór (biała sekcja) i rozkład błędów w stosie na interfejsie. Spośród nich atom jest zabarwiony zgodnie z centralnym parametrem symetrii, niebieski atom znajduje się w idealnym środowisku FCC, a czerwony atom jest w błędzie w stosie lub w bliźniaku.

Rysunek 4 (a) Widok z góry atomów Cu i Ag wzdłuż interfejsu: (ai) interfejs COC, (a.ii) interfejs TO, (b) widok z boku wzdłuż kierunku X = <011>: (bi) w COC W interfejs i przypadek, spójny region naprzemiennie z nieodłącznym regionem błędu stosu (ISF), (b.ii) interfejs TO, a obszar podwójnej defektu ciągle istnieje w warstwie Cu i warstwie Ag.

Rycina 5 pokazuje krzywą naprężenie-odkształcenie i stosunek atomowy bliźniaków w funkcji odkształcenia. Dzięki analizie odkryli, że interfejs może bezpośrednio lub pośrednio indukować zarodkowanie podwójnych dyslokacji poprzez dyslokacje Lomeru oraz w jaki sposób heterogeniczna struktura interfejsu wpływa na różne etapy procesu mechanicznego twinningu, wpływając w ten sposób na tworzenie tantalu w nanostrukturalnym Cu / Ag. Wielkość kryształu. Ta metoda w skali atomowej zapewnia przydatne podstawy teoretyczne do mechanicznego procesu twinningu w kompozytach w nanoskali.

Rycina 5 (a) krzywa naprężenie-odkształcenie, (b) stosunek atomowy bliźniaków w funkcji odkształcenia

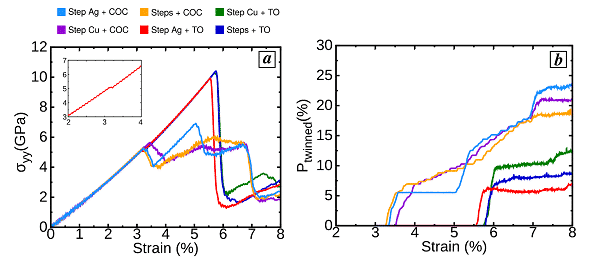
Projektowanie materiałów wielowarstwowych w celu dostosowania właściwości mechanicznych jest gorącym tematem przy kontrolowaniu mechanizmu deformacji, ponieważ twinning pozwala na włączenie właściwości mechanicznych nanowarstw i materiałów nanokrystalicznych. W związku z tym niniejsze badanie stanowi klucz do zrozumienia mechanizmu interakcji podwójnego interfejsu i potwierdza pogląd, że interfejsy heterofazowe promują twinning.

W przypadku bardzo drobnych warstwowych kompozytów zawierających metale strukturalne hcp o niskiej symetrii, duża liczba heterointerfejsów może skutecznie absorbować defekty, takie jak wakaty i atomy śródmiąższowe, spowodowane napromieniowaniem jądrowym, a same metale hcp mają niską gęstość, wytrzymałość właściwą i W ostatnich latach , sześciokątne materiały wielowarstwowe składające się z Ti, Zr, Mg i innych metali zaczęły przyciągać uwagę ludzi ze względu na ich wysoką sztywność właściwą oraz dobrą przewodność elektryczną i cieplną. Jednakże w porównaniu z metalami fcc i bcc o wysokiej symetrii struktury krystalicznej, metal hcp ma słabą zdolność do odkształcania plastycznego w temperaturze pokojowej, co ogranicza stosowanie powiązanych materiałów kompozytowych.

Oprócz przestrzennej i czasowej rozdzielczości skali atomowej, symulacja dynamiki molekularnej może opisać zachowanie w pełni scharakteryzowanego idealizowanego modelu nanokryształu, takie jak struktura międzyfazowa, siła napędowa i mechanizm atomowy; z drugiej strony może znajdować się na bardzo wysokich granicach i pozycjach ziarna. Duże odkształcenie plastyczne zaobserwowano przy niewłaściwej gęstości. Na przykład mechanizm zarodkowania dyslokacji, hartowanie granicy ziarna, bliźniacze mechaniczne w nanokrystalicznym Al, redukcja wielkości ziarna z przemieszczenia do mechanizmu deformacji opartej na granicy ziarna, obserwacja pasma ścinania i jego zależności powierzchni pękania.

Ponadto w praktycznym zastosowaniu i procesie badawczym, modelu teoretycznym dla różnych opisów i wyborów problemów, dynamika opracowała wiele gałęzi teoretycznych, na przykład Jian Han, Spencer L. Thomas z University of Pennsylvania i inni polegają na siła granicy Opis odłączenia podsumowuje pojęcie dynamiki granicy ziarna materiałów polikrystalicznych, Zheng Ma i in. badał kinetykę opadów FeCO3, a także kinetykę powierzchni / interfejsu.