As trincas por fadiga são geralmente o resultado de deformações plásticas periódicas em áreas locais. A fadiga é definida como “falha sob carga repetida ou outros tipos de condições de carga, e este nível de carga não é suficiente para causar falha quando aplicado apenas uma vez”. Esta deformação plástica ocorre não por causa da tensão teórica no componente ideal, mas porque a superfície do componente não pode ser realmente detectada.
August Wöhler é o pioneiro da pesquisa em fadiga e apresenta um método empírico. Entre 1852 e 1870, Wöhler estudou a falha progressiva de eixos ferroviários. Ele construiu o banco de ensaio mostrado na Figura 1. Este banco de ensaio permite que dois eixos ferroviários sejam girados e dobrados ao mesmo tempo. Wöhler traçou a relação entre a tensão nominal e o número de ciclos que levam à falha, que mais tarde é conhecido como diagrama SN. Cada curva ainda é chamada de linha aw ö hler. O método Sn ainda é o método mais utilizado atualmente. Um exemplo típico desta curva é mostrado na Figura 1.
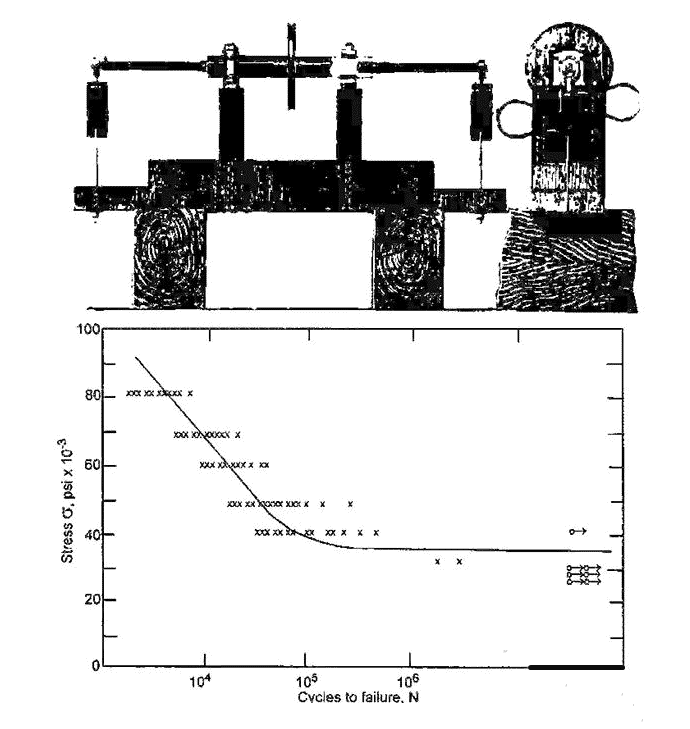
Vários efeitos podem ser observados através da linha de w ö hler. Primeiro, notamos que a curva SN abaixo do ponto de transição (cerca de 1000 ciclos) é inválida porque a tensão nominal aqui é elastoplástica. Mostraremos mais adiante que a fadiga é causada pela liberação de energia plástica de deformação de cisalhamento. Portanto, não há relação linear entre tensão e deformação antes da fratura e não pode ser usada. Entre o ponto de transição e o limite de fadiga (cerca de 107 ciclos), a análise baseada em Sn é válida. Acima do limite de fadiga, a inclinação da curva diminui acentuadamente, de modo que essa região é frequentemente chamada de região de “vida infinita”. Mas este não é o caso. Por exemplo, a liga de alumínio não terá vida infinita, e mesmo o aço não terá vida infinita sob carga de amplitude variável.
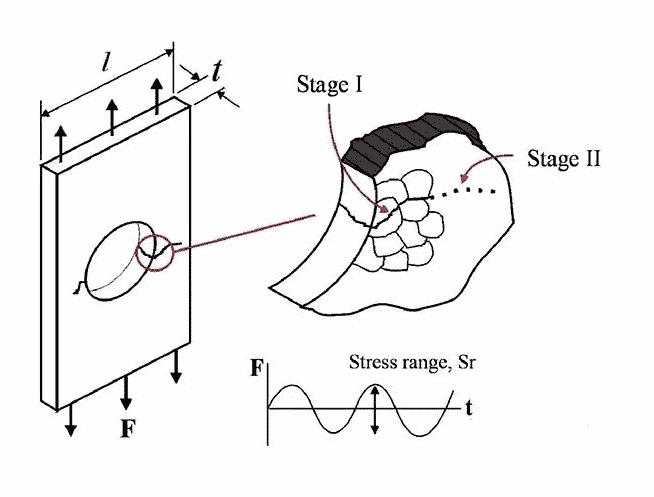
Com o surgimento da moderna tecnologia de amplificação, as pessoas podem estudar as rachaduras de fadiga com mais detalhes. Sabemos agora que o surgimento e propagação de trincas de fadiga podem ser divididos em duas etapas. No estágio inicial, a trinca se propaga em um ângulo de cerca de 45 graus em relação à carga aplicada (ao longo da linha de tensão de cisalhamento máxima). Após cruzar dois ou três contornos de grão, sua direção muda e se estende ao longo da direção de cerca de 90 graus em relação à carga aplicada. Esses dois estágios são chamados de rachadura de estágio I e rachadura de estágio II, conforme mostrado na Figura 2.
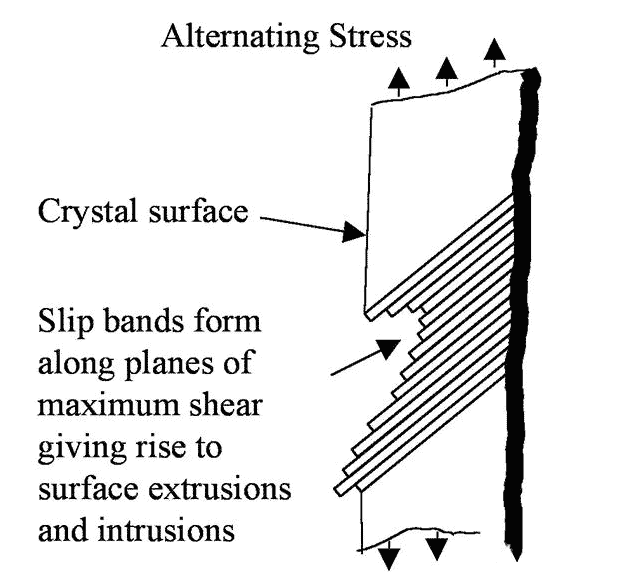
Se observarmos uma trinca estágio I em alta ampliação, podemos ver que a tensão alternada levará à formação de uma banda de deslizamento contínua ao longo do plano de cisalhamento máximo. Essas bandas deslizantes deslizam para frente e para trás, como um baralho de cartas, resultando em superfícies irregulares. A superfície côncava finalmente forma uma trinca “brotante”, como mostrado na Figura 3. Na fase I, a trinca se expandirá neste modo até atingir o contorno de grão e parará temporariamente. Quando energia suficiente é aplicada aos cristais adjacentes, o processo continuará.
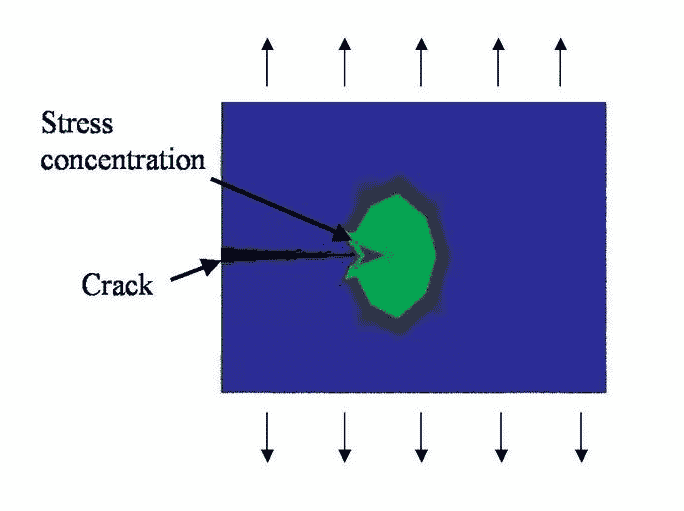
Após cruzar dois ou três contornos de grão, a direção de propagação da trinca agora entra no modo fase II. Neste estágio, as propriedades físicas de propagação de trincas mudaram. A própria trinca constitui um macro obstáculo ao fluxo de tensões, causando alta concentração de tensões plásticas na ponta da trinca. Conforme mostrado na Figura 4. Deve-se notar que nem todas as trincas do estágio I irão evoluir para o estágio II.
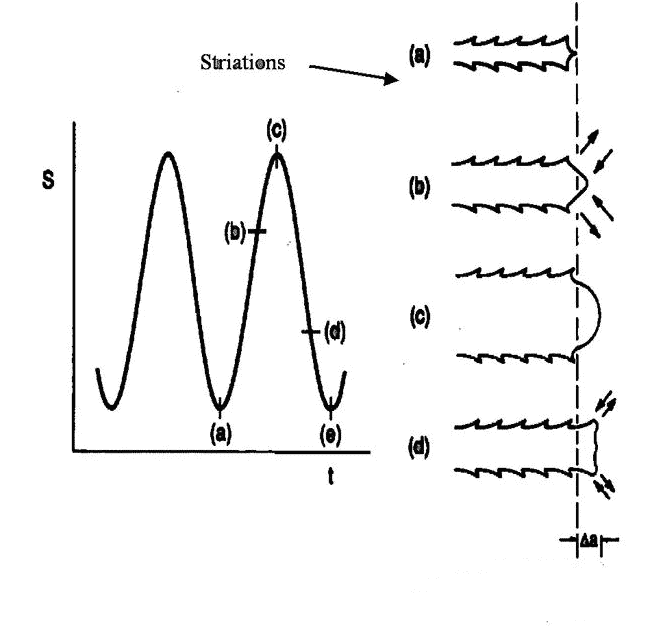
Para entender o mecanismo de propagação do estágio II, precisamos considerar a situação da seção transversal da ponta da trinca durante o ciclo de tensões. Conforme mostrado na Figura 5. O ciclo de fadiga começa quando a tensão nominal está no ponto “a”. À medida que a intensidade da tensão aumenta e passa pelo ponto “B”, notamos que a ponta da trinca se abre, resultando em deformação plástica por cisalhamento local, e a trinca se estende até o ponto “C” no metal original. Quando a tensão de tração diminui através do ponto “d”, observamos que a ponta da trinca se fecha, mas a deformação plástica permanente deixa um único serrilhado, a chamada “linha de corte”. Quando todo o ciclo termina no ponto “e”, observamos que a trinca agora aumentou o comprimento “Da” e formou linhas de seção adicionais. Entende-se agora que a faixa de crescimento da trinca é proporcional à faixa de deformação elástica-plástica aplicada na ponta da trinca. Uma faixa de ciclo maior pode formar um Da maior.
Fatores que afetam a taxa de crescimento de trincas por fadiga
A influência dos seguintes parâmetros na taxa de crescimento de trincas por fadiga é estudada e explicada conceitualmente:
1 Tensão de cisalhamento
A partir do diagrama, podemos ver que uma certa “quantidade” de tensão de cisalhamento é liberada durante a mudança periódica da resistência da tensão nominal. E quanto maior a gama de mudanças de estresse, maior a energia liberada. Através da curva SN mostrada na Figura 1, podemos observar que a vida em fadiga diminui exponencialmente com o aumento da faixa do ciclo de tensão.
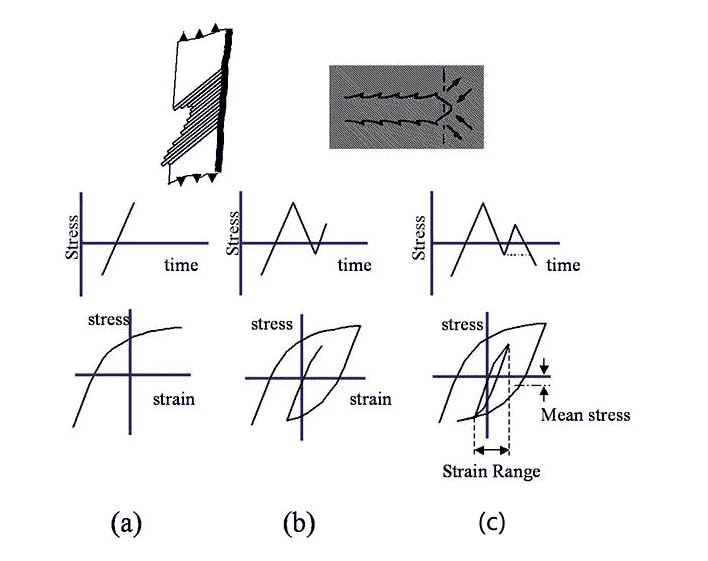
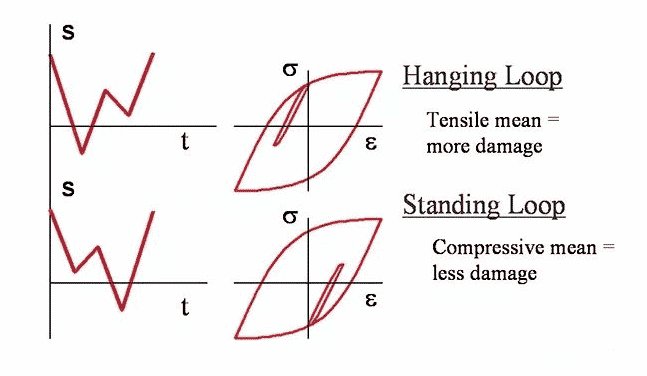
2 estresse médio
A tensão média (tensão residual) também é um fator que afeta a taxa de falha por fadiga. Conceitualmente, se a tensão de expansão for aplicada à trinca fase II, a trinca será forçada a abrir, então qualquer ciclo de tensão terá um efeito mais significativo. Pelo contrário, se a tensão de compressão média for aplicada, a trinca será forçada a fechar, e qualquer ciclo de tensão precisa superar a tensão de pré-compressão antes que a trinca possa continuar a se expandir. Conceitos semelhantes também se aplicam às trincas do estágio I.
3 acabamentos de superfície
Como as trincas de fadiga geralmente aparecem primeiro na superfície dos componentes onde há defeitos, a qualidade da superfície afetará seriamente a probabilidade de ocorrência de trincas. Embora a maioria das amostras de teste de material tenha acabamento espelhado, elas também alcançarão a melhor vida à fadiga. De fato, a maioria dos componentes não pode ser comparada com as amostras, então precisamos modificar as propriedades de fadiga. O acabamento superficial tem um efeito maior na fadiga de componentes submetidos a ciclos de tensão de baixa amplitude.
4 tratamento de superfície
O tratamento de superfície pode ser usado para aumentar a resistência à fadiga dos componentes. O objetivo do tratamento de superfície é formar tensões de compressão residuais na superfície. Sob o período de baixa amplitude, a tensão na superfície é obviamente baixa e até mantém o estado de compressão. Portanto, a vida de fadiga pode ser significativamente prolongada. No entanto, como apontamos, esta situação só é válida para componentes sujeitos a ciclos de tensão de baixa amplitude. Se for aplicado um período de alta amplitude, a pré-compressão será superada pelo período de alta amplitude e suas vantagens serão perdidas. Tal como acontece com a qualidade da superfície, o impacto do tratamento de superfície pode ser demonstrado por modelagem.







