Первый принцип на самом деле является философским термином, выдвинутым древнегреческим философом Аристотелем: в каждой системе есть базовое суждение, которое не может быть нарушено или удалено. Первый принцип на самом деле является философским термином, выдвинутым древнегреческим философом Аристотелем: В каждой системе есть базовое предложение, которое нельзя нарушать или удалять.
Рисунок 1 Аристотель

В области материаловедения первый принцип касается принципа взаимодействия атомного ядра и электрона и его основного закона движения. Используя квантовую механику, исходя из конкретных требований, после ряда приближений волновое уравнение Шредингера решается непосредственно для получения электронной структуры. Тем самым физические и химические свойства системы точно получены, а состояние и свойства микроскопической системы предсказаны. Однако процесс решения очень сложен. По этой причине Борн-Оппенгеймер предложил адиабатическое приближение, которое заключается в рассмотрении всей проблемы движения электронов и ядер. Учитывая движение ядра в мгновенном положении, учитывая движение ядра, электрон не учитывается. Специфическое распределение пространства. Для N-электронных систем решение все еще очень сложно, поэтому предлагается приближение одного электрона, то есть рассматривается только один электрон, а другие электроны обрабатываются аналогично некоторой форме потенциального поля, которая преобразуется в один. Электронная задача - приближение среднего поля [1, 2].
Первый принцип заключается в решении уравнения Шредингера, описывающего закон движения микроскопических частиц, путем самосогласованного расчета на основе адиабатического приближения и одноэлектронного приближения. Приближение Хартри-Фока является своего рода приближением среднего поля, которое игнорирует взаимодействие между электронами и рассматривает электроны как движения в среднем потенциальном поле ионного потенциального поля и других электронов. Аппроксимация ограничивает точность расчета. В 1964 году Хоэнберг и Кон предложили теорию функционала плотности, которая тонко выражает связанный с обменом потенциал между электронами как форму функционала плотности, так что свойства материала могут быть определены из плотности электронов. С тех пор Кон и Шам (Shen Lujiu) получили одноэлектронное уравнение в теории функционала плотности, а именно уравнение Кона-Шама (KS), которое практически применяет теорию функционала плотности [3, 4]. Эта статья суммирует последние достижения приложения первых принципов в следующих аспектах:
Расчет параметров кристаллической структуры и конфигурации
Кристаллическая структура является основой для понимания самых основных свойств материалов, особенно для выявления взаимосвязи между микроструктурой материалов и внутренними свойствами упругости, электронов, фононов и термодинамики.
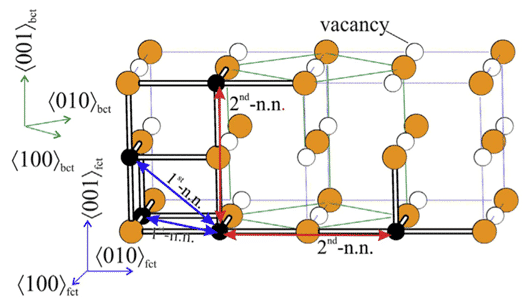
Leineweber, T. Hickel et al. использовал исчерпывающий метод для расчета DFT возможных структур Fe4N и Fe4C, учитывая ГЦК-расположение атомов Fe и положение атомов N / C на октаэдрах, где часть структуры может проходить Бэйна. Искажение становится стабильным, и атом С проявляет последовательность типа Зенера в ОЦК, как показано на рис. 2, и выявляет характерную разницу в ориентационной тенденции атомов внедрения, что согласуется с экспериментально наблюдаемой разницей аустенитной структуры [5 ].
Рисунок 2 fct (гранецентрированное тетрагональное) расположение двух атомов Fe (синий)
Расчет фазовой устойчивости сплава
Метод полной энергии из первых принципов, основанный на плоской волне сверхпотенциала, используется для изучения структуры кристаллической фазы, и получается термодинамическая стабильность микроструктуры различных порядков упаковки, так что предсказывается, что наиболее стабильная структура, которая может существовать, быть новым дизайном и разработкой. Важное средство материалов.
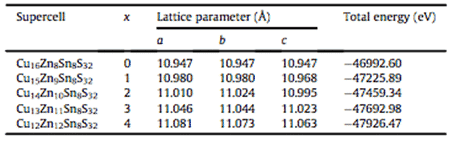
Например, Жилин Ли, Чуньян Ся и др. провел первопринципное исследование фазовой стабильности Cu2ZnSnS4, тонкопленочного материала слоя поглотителя солнечных батарей, основанного на теории функционала плотности (DFT), с использованием PBE в обобщенном приближении градиента (GGA). Параметры решетки и полная энергия системы сплава Cu-Zn-Sn-S были рассчитаны по обменному корреляционному потенциалу, а также были установлены модель расчета и энергия генерации возможных фаз в сплаве Cu-Zn-Sn-S. Результаты показаны на рис. 3 и в таблице 1. Как показано, это исследование дает руководство по разработке сплавов Cu-Zn-Sn-S для тонкопленочных композитных солнечных элементов. Модель и метод расчета также могут быть распространены на предсказание фазовой стабильности других систем сплавов [6].
Рис.3 Модель сверхрешеточной структуры дефектов замещения 64 ZnCu
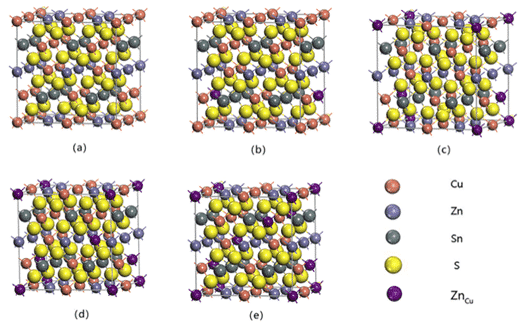
Таблица 1 Оптимизированная структура сверхрешетки и результаты расчета полной энергии
Электронная структура
Для стабильных структур вычисление распределения валентной электронной плотности материалов важно для понимания степени связи и ионизации между атомами.
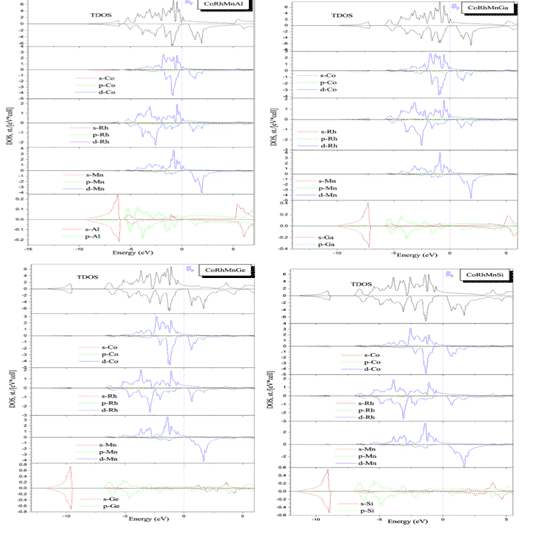
Бенкабу и Х. Рашед и др. использовал первый принцип для расчета четвертичных сплавов Гейслера CoRhMnZ (Z = Al, Ga, Ge и Si) (класс интерметаллических соединений, которые можно описать как X2YZ или XX0YZ, где X, X0 и Y — элемент переходного металла, Z представляет собой элемент группы III, IV или V, обычно содержит неферромагнитные элементы, но соединение демонстрирует ферромагнитную) электронную структуру, рассчитанную с использованием метода линейных прикрепленных плоских волн с полным потенциалом (FLAPW) и приближения GGA-PBE. На рисунке 4 показаны результаты расчетов плотности состояний для соответствующих структур, показывающие, что эти соединения обладают полуметаллическими ферромагнетиками в нескольких состояниях, соединения CoRhMnGe и CoRhMnSi, а их магнитные моменты в основном соответствуют закону Слейтера-Полинга, что указывает на их полуметаллическую структуру. характеристики. Высокая спиновая поляризация, помимо CoRhMnSi, эти соединения устойчивы в структуре YI [7].
Рис. 3 Общая плотность и локальная плотность состояний устойчивых структур CoRhMnZ (Z = Al, Ga, Ge и Si)
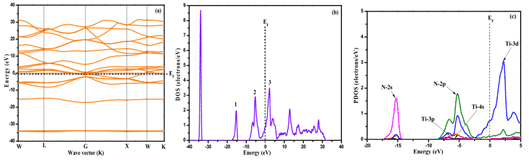
Song et al. использовал первый принцип для изучения электронной структуры пленки TiN. Как показано на рисунке 4, полоса была смоделирована программой Studio Studio (MS), и были рассчитаны полная плотность состояний (DOS), диэлектрическая функция и поглощение. И отражательная способность.
Результаты показывают, что энергия Ферми (EF) проходит через энергетическую зону с плотным распределением уровней энергии, а полная плотность состояний пересекается с EF, что указывает на то, что TiN определяется электронными свойствами состояния Ti-3d, чтобы иметь металлоидные свойства [8 ].
Рис. 4 Структура энергетической зоны пленки TiN (а), полная плотность (б) и локальная плотность (в)
Расчет механических свойств
Постоянная упругости Cij является основным параметром, описывающим механические свойства материалов. Он тесно связан с основными явлениями твердого тела, такими как межатомная связь, уравнения состояния и фононные спектры, а также с термодинамическими свойствами, такими как удельная теплоемкость, тепловое расширение, температура Дебая и параметры Грюнайзена. Связанный. Теоретически существует 21 независимая упругая константа Cij, но симметрия кубического кристалла уменьшает это значение только до 3 (C11, C12 и C44), а модуль сдвига G, модуль Юнга E и Пуассона выводятся из упругих констант. Соотношение n, затем оцените температуру Дебая по средней скорости звука Vm:
Где H - постоянная Планка, KB - постоянная Больцмана, Va - атомный объем, а Vm можно определить по продольным и поперечным скоростям звука vl и vt, полученным с помощью модуля сдвига G и модуля B объема в уравнении Навье. ,
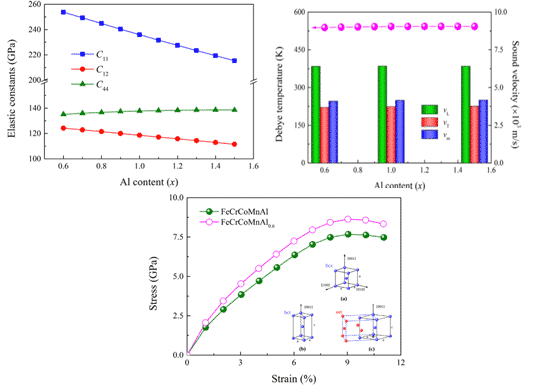
Например, Shuo Huang et al. объединил первый принцип для определения упругих параметров и идеальной прочности на разрыв фазы FeCrCoMnAlx (0.6≤≤1.5) с высокоэнтропийным сплавом с объемно-центрированным кубическим твердым раствором в направлении [001]. Результаты показаны на рис. 5. В рассматриваемом интервале композиций было установлено, что ОЦК-структура имеет более низкую энергию, чем ферромагнитное и парамагнитное состояния ГЦК и ГПУ-структур. Исходя из теоретической температуры Кюри, ожидается, что все сплавы будут ферромагнитными при комнатной температуре, а идеальная прочность на разрыв в направлении [001] ожидается равной 7,7 ГПа при максимальной деформации около 9%. Прочность может быть дополнительно увеличена путем снижения концентрации Al. [9].
Рис.5. Упругая постоянная, кривая Дебая и деформация напряжения высокоэнтропийного сплава FeCrCoMnAlx.
Расчет свойств поверхности или поверхности раздела
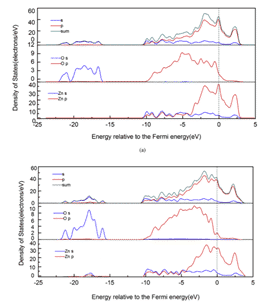
Недавно Ю. Лу и соавт. использовался композитный припой Sn9Zn-1Al2O3-xCu для пайки алюминиевого сплава 6061 и изучал влияние добавления элементов Cu и Al2O3 на характеристики пайки. Основываясь на теории теории функционала плотности (DFT) и GGA-PBE, первопринципные расчеты были выполнены для межфазной структуры, межфазной энергии, угла контакта и электронных свойств Al2O3 / Sn9Zn. Расчеты показывают, что Sn9Zn-1Al2O3-4.5Cu и Sn9Zn-1Al2O3-6Cu имеют стабильную структуру, и соответствующие результаты показаны на рисунках 6 и 7 [10].
Рис. 6. Контурные плоскости с различными различиями плотности заряда для разных структур: (a) Sn9Zn — 1Al2O3 , (b) Sn9Zn — 1Al2O3–4,5Cu
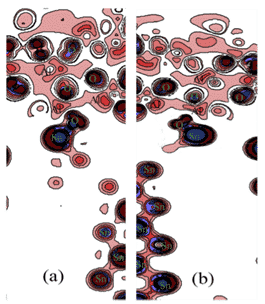
Рис. 7 Плотность локализованных состояний различных структур: (a) Sn9Zn-1Al2O3, (b) Sn9Zn-1Al2O3-4.5Cu
Другие приложения
Например, Kulwinder Kaur et al. использовали теорию функционала плотности (DFT) и теорию пропускания Больцмана для изучения высокотемпературных термоэлектрических свойств ГЦК HfRhSb. Рисунки 8 и 9 показывают рассчитанную структуру энергетической зоны и плотности состояний, а также некоторые физические параметры. Теория характеристик пропускания начинается с расчета зонной структуры, теории пропускания Больцмана в жесткой зоне и приближения постоянного времени релаксации (RTA). Приближение жестких рабочих характеристик (RBA) является эффективным инструментом для изучения взаимосвязи между зонной структурой и термоэлектрическим откликом [11].
Рисунок 8 (а) структура энергетической зоны (б) полная локальная плотность состояний (в) фононная дисперсия (г) фононная ДОС
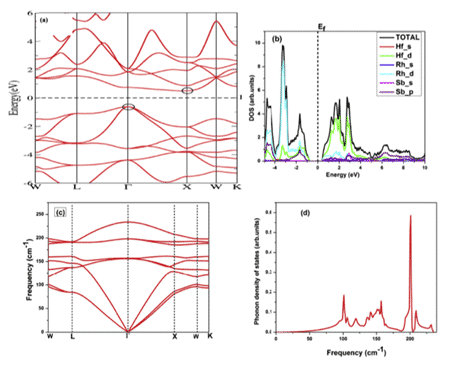
Рисунок 9 Коэффициент Зеебека, проводимость, теплопроводность и термоэлектрическая эффективность ZT как функция температуры

Ссылка
1. Гейзенберг В. Квантово-теоретическое переосмысление кинематических и механических соотношений [J]. Z Phys, 1925, 33: 879
2. Шрёдингер E, Quantisierung als eigenwertproblem I [J]. Ann der Phys, 1926, 9: 361
3. Хоэнберг П., Кон В. Неоднородный электронный газ [Дж]. Phys Rev B, 1964, 136 (3): 864
4. Кон В., Шам Л. Дж. Самосогласованные уравнения, включая обменные и корреляционные эффекты [J]. Phys Rev A, 1965, 140 (4): 1133
5.Leineweber, T. Hickel, B. Azimi-Manavi, SB Maisel , Кристаллические структуры Fe4C и Fe4N, проанализированные с помощью DFT-расчетов: исследованы межузельные надстройки на основе Fcc [J], Acta Materialia 140 (2017) 433-442
6.Жилин Ли, Чуньян Ся, Чжэнпин Чжан, Мэйлин Доу, Цзин Цзи, Е Сон, Цзинцзюнь Лю, Фэн Ван , Первопринципное исследование фазовой стабильности кестерита Cu2ZnSnS4 для тонкопленочных солнечных элементов со нестехиометрическим составом [J] , Журнал сплавов и соединений 768 (2018) 644-651
7. Бенкабу, Х. Рэйчед, А. Абделлауи, Д. Рэйчед, Р. Хената, М. Х. Элахмар, Б. Абидри, Н. Бенхетту, С. Бин-Омран , Электронная структура и магнитные свойства четвертичных сплавов Гейслера CoRhMnZ (Z = Al, Ga, Ge и Si) с помощью первопринципных расчетов [J] , Журнал сплавов и соединений 647 (2015) 276-286
8.Хуидзин Сонг, Пэн Гу, Синхуа Чжу, Цян Янь, Динъю Янг , Исследование электронной структуры и оптических свойств пленок TiN на основе принципа первого принципа [J] , Физика B: Конденсированное вещество 545 (2018) 197–202
9.Шу Хуан, Сяоцин Ли, Хе Хуан, Эрик Холмстроум, Левенте Витос, Механические характеристики высокоэнтропийных сплавов FeCrCoMnAlx из первоосновы [J], Химия материалов и физика 210 (2018) 37-42
10.Юй Лу, Ле Ма, Шу-Ён Ли, Вэй Цзуо, Чжи-цзян Цзи, Мин Дин addition Влияние добавления элемента Cu на межфазное поведение и механические свойства пайки Sn9Zn-1Al2O3 алюминиевых сплавов 6061: расчеты по первому принципу и экспериментальные исследования [J] , Журнал сплавов и соединений 765 (2018) 128-139
11.Кульвиндер Каур, Ранджан Кумар, Д.П. Рай, Многообещающий термоэлектрический отклик полуфазоновского соединения HfRhSb при высокой температуре: исследование первого принципа [J], Журнал сплавов и соединений 763 (2018) 1018-1023








