要很好地了解杨氏模量并在标题栏上回答这个问题,我们需要考虑材料如何获得弹性。
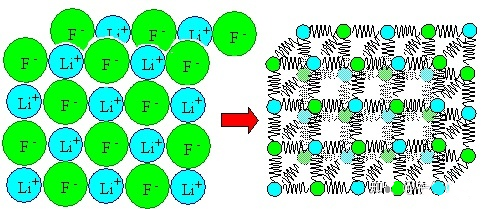
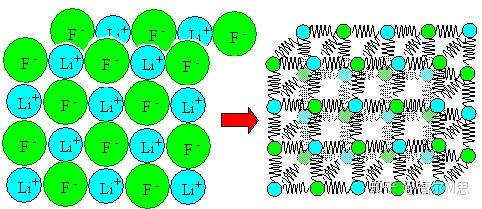
对于金属材料,我们知道它们的内部是由原子组成的,许多原子有规律地排列形成晶体,许多晶粒结合在一起形成我们平时看到的金属。
弹性是否来自谷物之间的相互作用?显然不是,因为单晶和非晶都具有弹性。
因此,弹性可能来自原子之间的相互作用。
为了尽可能简单方便,我们尽量不引入复杂的概念或数学公式。让我们从 最简单的双原子模型.
杨氏模量的双原子模型
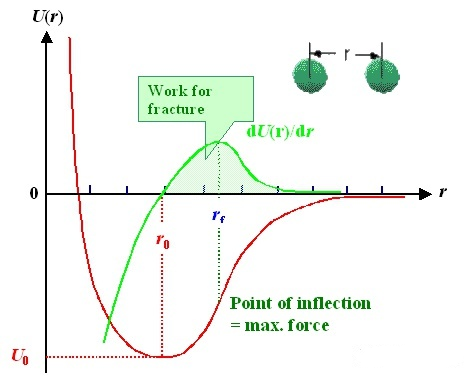
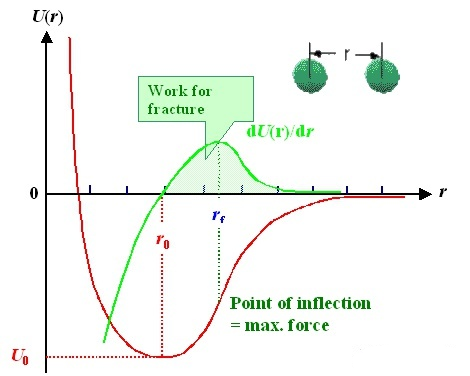
双原子模型:两个原子之间的相互作用可以用势函数(红线)来描述。横轴是两个原子之间的距离“r”,纵轴是势能U(r);通过推导势函数可以获得相互作用力(绿线)。值得注意的是,两个原子之间存在一个平衡位置r0r_{0},其中相互作用力F=0,势能最低;换句话说,当你离开这个位置时,无论是向左还是向右,都会有一股力量试图把它拉回来。
就像弹簧一样,自然状态下就有这样的平衡位置。无论是挤压弹簧还是拉伸弹簧,松开手后弹簧仍会弹回原位。
这就是原子层面的弹性来源!
当然,实际的金属或其他材料内部有很多原子。这些原子相互作用可以简单地理解为一对原子相互作用的叠加。
杨氏模量与其他参数关系分析
一般来说,我们可以简单地假设这个势函数具有以下形式:
上述函数有四个可变参数,即平衡位置R0R_{0}, 投标能量U0U_{0}, 以及参数 N 和 M。上述参数可能因不同种类的原子而异。
现在我们把这两个原子作为一个独立的系统,对它们进行拉伸或压缩。
为了改变平衡位置附近两个原子之间的距离,要施加的力 F
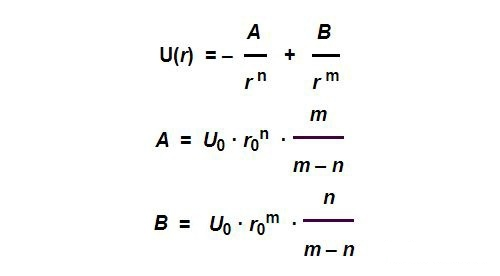
为了对应杨氏模量,我们需要将其变为σ= E ε 的形式,两边除以一个r02r_{0}^{2}并代入上式假装操作:
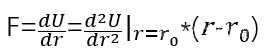
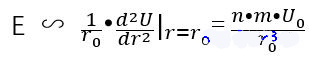
结论
也就是说,杨氏模量E主要受N、m、u0u_{0}、r0r_{0}的影响。原子种类和温度会影响这些参数。不同原子种类的影响是显而易见的,所有参数都会发生变化。温度的影响似乎不太明显。
要观察温度的影响,我们必须回到势函数曲线本身。由于势函数不是完美的对称曲线,当温度升高时,意味着原子运动更加剧烈,运动幅度变大,如热胀冷缩。此时,平衡位置r0r_{0}会发生偏移,如下图绿线所示。
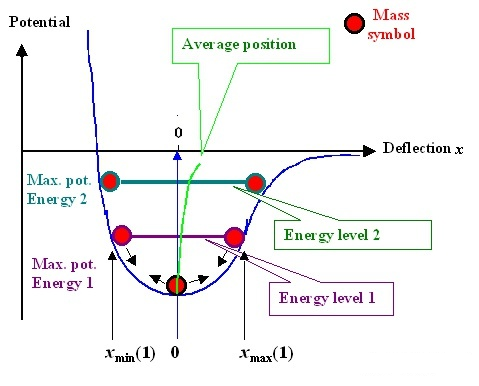
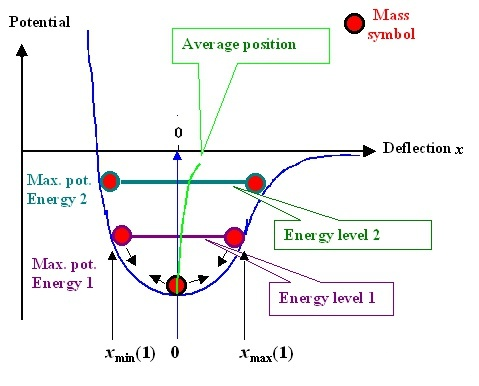
可以证明原子总是在运动的。当温度较高时,平衡位置r0r_{0}越大,材料的体积增大,杨氏模量减小。
回到我们最初的问题,不同等级钢中的铁原子数可以占到90%以上。即使与纯铁相比,原子间的相互作用力变化也不大,因此其杨氏模量几乎不受合金成分变化的影响;同样,无论微观结构发生变化还是加工硬化,原子的重排都不会改变原子间的作用力,因此不会影响杨氏模量。
除了杨氏模量外,还可以推导出完美晶体的熔点、热膨胀系数和拉伸强度等物理量。
至于高弹性状态下的橡胶杨氏模量随温度升高而增大的异常现象,是因为橡胶弹性的来源与常规材料不同。








