疲劳裂纹一般是局部区域周期性塑性变形的结果。疲劳被定义为“在重复负载或其他类型负载条件下的失效,并且该负载水平在仅应用一次时不足以导致失效”。这种塑性变形的发生不是因为理想元件上的理论应力,而是因为不能实际检测到元件表面。
August Wöhler 是疲劳研究的先驱,他提出了一种经验方法。 1852 年至 1870 年间,沃勒研究了铁路车轴的渐进式故障。他建造了图 1 所示的试验台。该试验台使两个铁路车轴能够同时旋转和弯曲。 Wöhler 绘制了标称应力与导致失效的循环次数之间的关系,这就是后来的 SN 图。每条曲线仍称为 awöhler 线。 Sn 法仍然是当今使用最广泛的方法。该曲线的一个典型例子如图 1 所示。
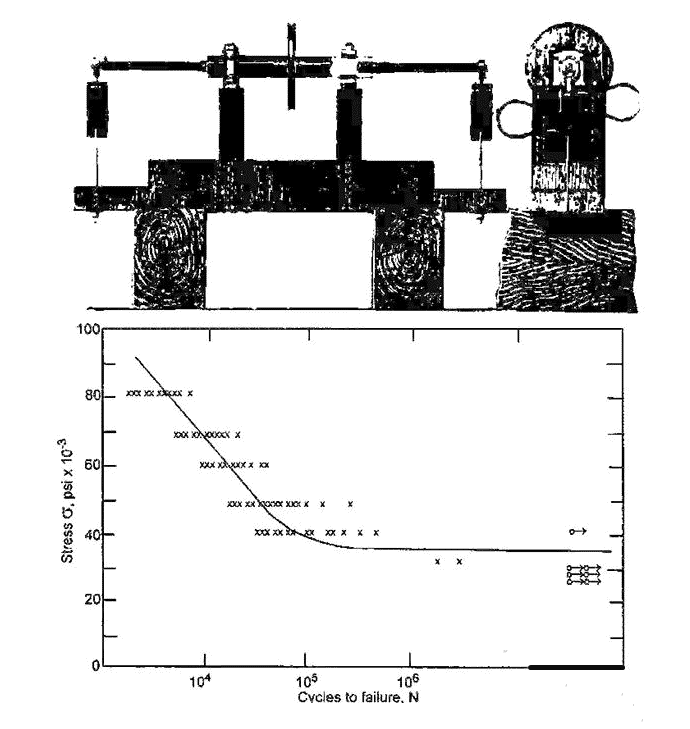
通过 wöhler 线可以观察到几种影响。首先,我们注意到低于过渡点(大约 1000 个循环)的 SN 曲线是无效的,因为这里的标称应力是弹塑性的。稍后我们将说明疲劳是由塑性剪切应变能的释放引起的。因此,断裂前的应力和应变之间没有线性关系,不能使用。在过渡点和疲劳极限之间(大约 107 个循环),基于 Sn 的分析是有效的。在疲劳极限以上,曲线的斜率急剧下降,因此该区域通常被称为“无限寿命”区域。但这种情况并非如此。例如,铝合金不会有无限寿命,甚至钢在变幅载荷下也不会有无限寿命。
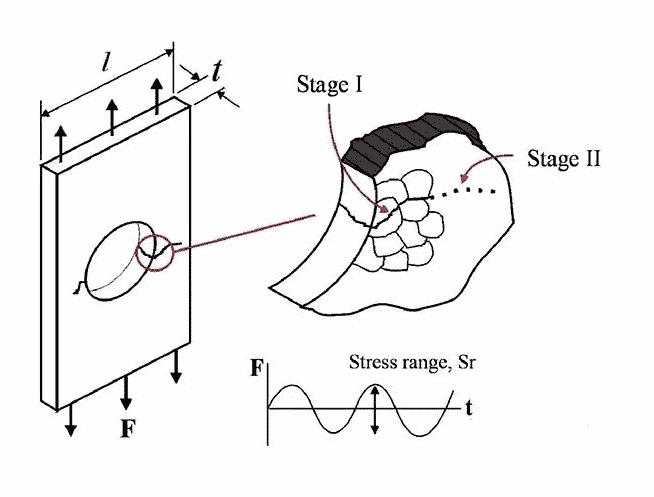
随着现代放大技术的出现,人们可以更详细地研究疲劳裂纹。我们现在知道,疲劳裂纹的产生和扩展可以分为两个阶段。在初始阶段,裂纹以与施加载荷成约 45 度的角度(沿最大剪应力线)扩展。在穿过两个或三个晶界后,其方向发生变化,并沿相对于施加载荷成约 90 度的方向延伸。这两个阶段称为Ⅰ期裂纹和Ⅱ期裂纹,如图2所示。
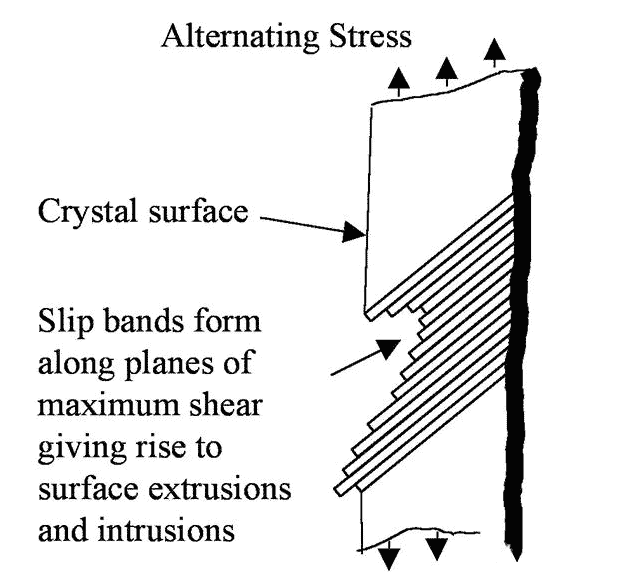
如果我们在高倍率下观察 I 期裂纹,我们可以看到交变应力会导致沿最大剪切面形成连续滑移带。这些滑带来回滑动,就像一副纸牌一样,导致表面不平整。凹面最终形成“萌芽”裂纹,如图 3 所示。在第一阶段,裂纹会以这种方式扩展,直到遇到晶界并暂时停止。当足够的能量施加到相邻的晶体上时,该过程将继续进行。
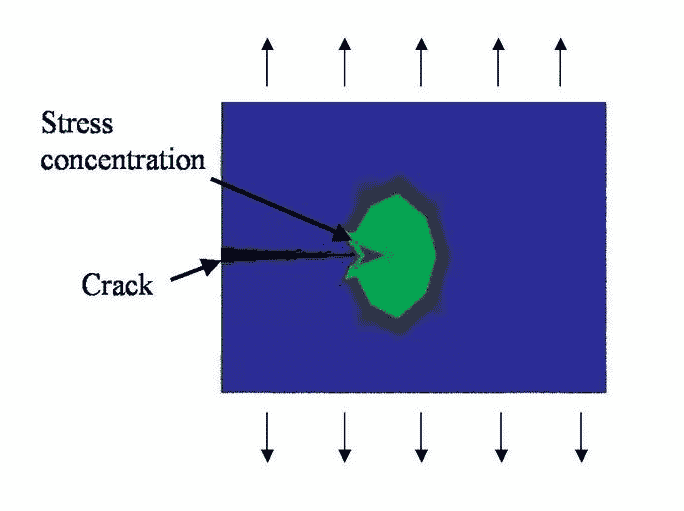
穿过两个或三个晶界后,裂纹扩展方向现在进入第二阶段模式。在这个阶段,裂纹扩展的物理性质发生了变化。裂纹本身构成了应力流动的宏观障碍,导致裂纹尖端的高塑性应力集中。如图 4 所示。需要注意的是,并不是所有的 I 期裂缝都会发展到 II 期。
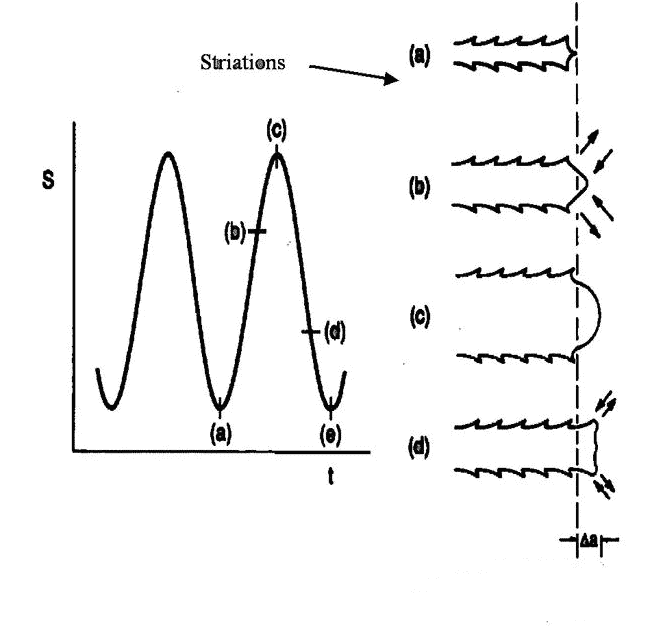
为了理解第二阶段的扩展机制,我们需要考虑应力循环过程中裂纹尖端截面的情况。如图 5 所示。当名义应力位于“a”点时,疲劳循环开始。随着应力强度的增加并通过“B”点,我们注意到裂纹尖端张开,导致局部塑性剪切变形,裂纹延伸到原始金属中的“C”点。当拉应力通过“d”点减小时,我们观察到裂纹尖端闭合,但永久塑性变形留下了独特的锯齿,即所谓的“切割线”。当整个循环在“e”点结束时,我们观察到裂缝现在增加了“Da”长度并形成了额外的截面线。现在可以理解,裂纹扩展的范围与所施加的弹塑性裂纹尖端应变的范围成正比。较大的循环范围可以形成较大的Da。
影响疲劳裂纹扩展速率的因素
对下列参数对疲劳裂纹扩展速率的影响进行了研究和概念解释:
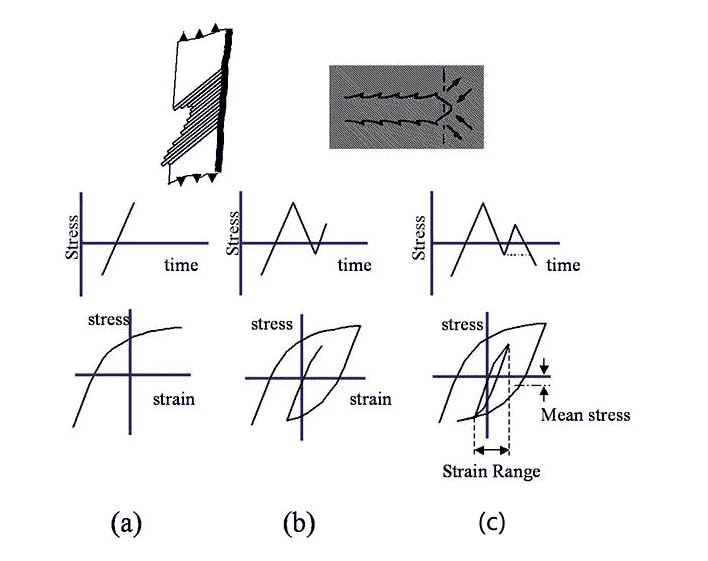
1剪应力
从图中我们可以看出,在名义应力强度的周期性变化过程中,会释放出一定“量”的剪应力。并且应力变化范围越大,释放的能量越大。通过图1所示的SN曲线可以看出,疲劳寿命随着应力循环范围的增加呈指数下降。
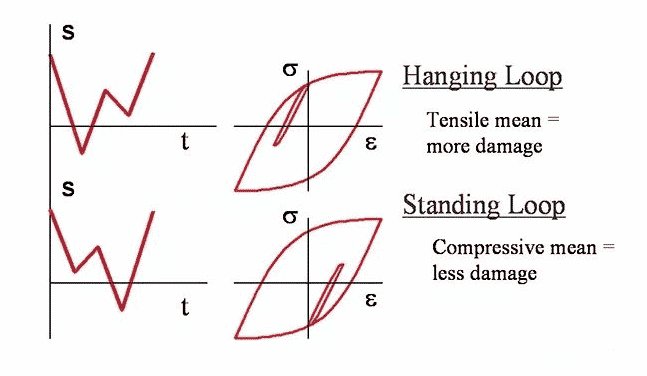
2 平均压力
平均应力(残余应力)也是影响疲劳失效率的一个因素。从概念上讲,如果向 II 相裂纹施加膨胀应力,则裂纹将被迫张开,因此任何应力循环都会产生更显着的影响。相反,如果施加平均压应力,裂纹将被迫闭合,任何应力循环都需要克服预压应力,裂纹才能继续扩展。类似的概念也适用于第一阶段的裂缝。
3 表面处理
因为疲劳裂纹通常首先出现在有缺陷的部件表面,表面质量会严重影响裂纹发生的概率。尽管大多数材料测试样品都具有镜面光洁度,因此它们也会达到最佳的疲劳寿命。事实上,大多数部件无法与样品进行比较,因此我们需要修改疲劳特性。表面光洁度对承受低振幅应力循环的部件的疲劳影响更大。
4 表面处理
表面处理可用于增强部件的抗疲劳性。表面处理的目的是在表面形成残余压应力。在低振幅周期下,表面应力明显较低,甚至保持压缩状态。因此,可以显着延长疲劳寿命。然而,正如我们所指出的,这种情况仅适用于受到低振幅应力循环的组件。如果应用高振幅周期,预压缩将被高振幅周期克服,其优势将丧失。与表面质量一样,表面处理的影响可以通过建模来显示。