第一个原则实际上是古希腊哲学家亚里斯多德提出的一个哲学术语:每个体系中都有一个基本命题,不能被违反或删除。第一个原理实际上是古希腊哲学家亚里士多德提出的一个哲学术语:每个系统都有一个基本命题,不能被违反或删除。
图1亚里斯多德

在材料科学领域,第一原理是指原子核与电子相互作用的原理及其基本运动规律。使用量子力学,根据特定的要求,经过一系列近似后,直接求解薛定inger波动方程以获得电子结构。从而准确地获得了系统的物理和化学性质,并预测了微观系统的状态和性质。但是,解决过程非常困难。因此,Born-Oppenheimer提出了一种绝热近似,即将整个问题考虑到电子和原子核的运动中。考虑到原子核在瞬时位置的运动,考虑到原子核的运动,不考虑电子。空间的具体分布。对于N个电子系统,解决方案仍然非常困难,因此提出了一个电子近似方法,即仅考虑一个电子,而将其他电子以类似于某种形式的势场的方式处理,将其转换为单个电子。电子问题是平均场近似[1,2]。
第一个原理是在绝热近似和单电子近似的基础上,通过自洽计算来求解描述微观粒子运动规律的薛定ding方程。 Hartree-Fock近似是一种平均场近似,它忽略电子之间的相互作用,并将电子视为离子势场和其他电子的平均势场中的运动。近似值限制了计算的准确性。 1964年,Hohenberg和Kohn提出了密度泛函理论,该理论巧妙地将电子之间的交换相关电势表示为密度泛函的一种形式,因此可以根据电子密度来确定材料的特性。从那时起,Kohn和Sham(Shen Lujiu)在密度泛函理论中获得了单电子方程,即Kohn-Sham(KS)方程,这使得密度泛函理论得到了实际应用[3,4]。本文从以下几个方面总结了第一原则的最新应用进展:
晶体结构参数和构型的计算
晶体结构是了解材料最基本特性的基础,尤其是揭示材料的微观结构与弹性,电子,声子和热力学的固有特性之间的关系。
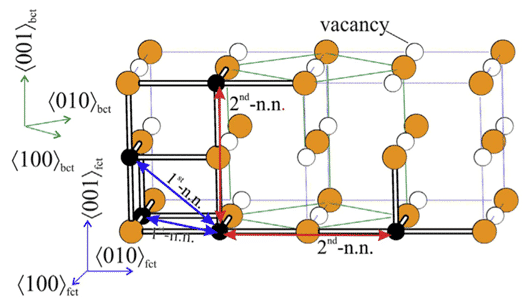
Leineweber和T. Hickel等。考虑到Fe原子的fcc排列和八面体上N / C原子的位置(其中部分结构可以通过贝恩),我们使用了详尽的方法对Fe4N和Fe4C的可能结构进行DFT计算。如图2所示,畸变变得稳定,C原子在bcc中表现出一个齐纳型序列,并揭示了间隙原子取向趋势的特征差异,这与实验观察到的奥氏体结构差异一致[5]。 ]。
图2两个铁原子的fct(面心四边形)排列(蓝色)
合金相稳定性的计算
采用基于超势平面波的第一性原理全能量方法研究了晶体的相结构,并获得了不同堆积顺序的微观结构的热力学稳定性,从而预测了可能存在的最稳定的结构。进行新的设计和开发。材料的重要手段。
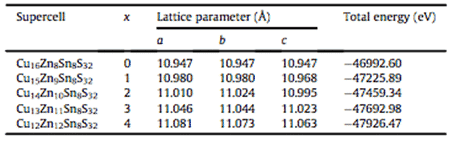
例如,李志林,夏春阳等。基于密度泛函理论(DFT),在广义梯度近似(GGA)下使用PBE,对薄膜太阳能电池吸收层材料Cu2ZnSnS4的相稳定性进行了第一性原理研究。利用交换相关势计算了Cu-Zn-Sn-S合金的晶格参数和总能,建立了Cu-Zn-Sn-S合金的计算模型和可能相的产生能。结果显示在图3和表1中。如图所示,该研究为薄膜复合太阳能电池的Cu-Zn-Sn-S合金设计提供了指导。该模型和计算方法还可以扩展到其他合金系统的相稳定性预测[6]。
图3 64个ZnCu置换缺陷的超晶格结构模型
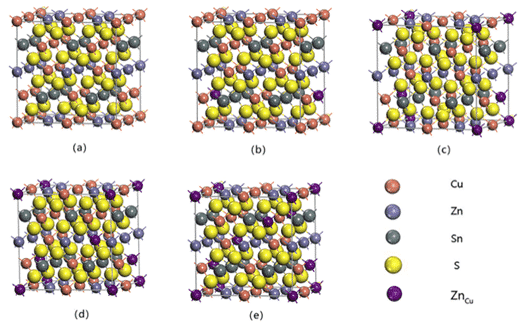
表1优化的超晶格结构及总能量计算结果
电子结构
对于稳定的结构,计算材料的价电子密度分布对于理解原子之间的键合和电离程度很重要。
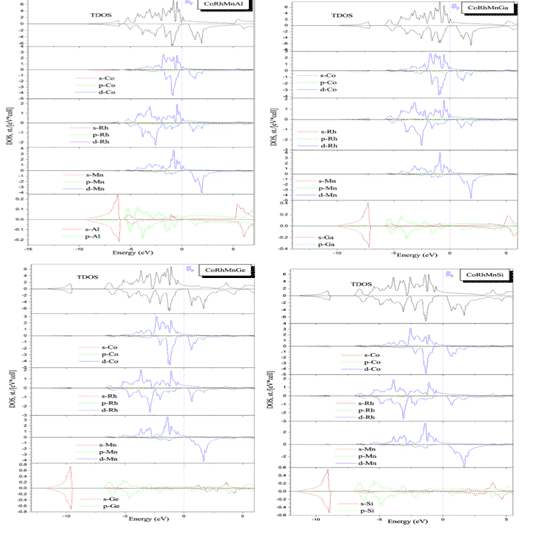
Benkabou 和 H. Rached 等人。用第一原理计算四元CoRhMnZ(Z=Al、Ga、Ge和Si)Heusler合金(一类金属间化合物,可描述为X2YZ或XX0YZ,其中X、X0和Y为过渡金属元素,Z是III、IV或V族元素,一般含有非铁磁性元素,但化合物呈现铁磁性)电子结构,采用全势线性贴附平面波法(FLAPW)和GGA-PBE近似计算。图 4 显示了相应结构的态密度计算结果,表明这些化合物在少数状态下表现出半金属铁磁体,CoRhMnGe 和 CoRhMnSi 化合物的磁矩基本符合 Slater-Pauling 定律,表明它们是半金属的。特性。高自旋极化,除了CoRhMnSi,这些化合物在YI结构中是稳定的[7]。
图3 CoRhMnZ(Z = Al,Ga,Ge和Si)稳定结构的状态的总密度和局部密度
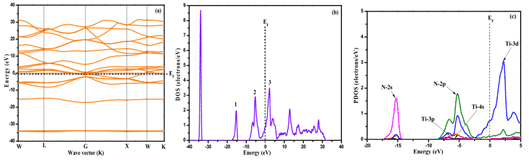
宋等。用第一原理研究了TiN薄膜的电子结构。如图4所示,该频带由Studio Studio(MS)程序模拟,并计算了总状态密度(DOS),介电函数和吸收率。和反射率。
结果表明,费米能量(EF)穿过能级分布密集的能带,且态的总密度与EF相交,表明TiN是由Ti-3d态的电子性质决定的具有准金属性质[8] ]。
图4 TiN薄膜的能带结构(a),全密度(b)和局部密度(c)
力学性能的计算
弹性常数Cij是描述材料力学性能的基本参数。它与原子间键合、状态方程和声子光谱等基本固体现象,以及比热、热膨胀、德拜温度和Grüneisen参数等热力学性质密切相关。有关的。理论上,有 21 个独立的弹性常数 Cij,但立方晶体的对称性将这个值减少到只有 3 个(C11、C12 和 C44),而剪切模量 G、杨氏模量 E 和泊松都是从弹性常数推导出来的。比率 n,然后从平均声速 Vm 估计德拜温度:
其中H是普朗克常数,KB是玻尔兹曼常数,Va是原子体积,而Vm可以通过Navier方程中的剪切模量G和体积模量B获得的纵向和横向声速vl和vt来确定。 。
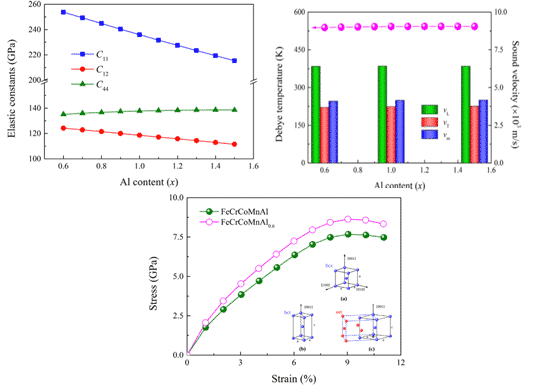
例如,硕硕等。结合第一个原理,确定了[001]方向上FeCrCoMnAlx(0.6≤≤1.5)高熵合金体心立方固溶体相的弹性参数和理想抗拉强度。结果如图5所示。在所考虑的组成范围内,发现bcc结构的能量低于fcc和hcp结构的铁磁和顺磁态。基于理论居里温度,预计所有合金在室温下均为铁磁性,并且在最大应变约为9%时,在[001]方向上的理想抗拉强度预计为7.7 GPa。通过降低Al的浓度,可以进一步提高强度。 [9]。
图5 FeCrCoMnAlx高熵合金的弹性常数,德拜温度和应力-应变曲线
表面或界面特性的计算
最近,于露等。用Sn9Zn-1Al2O3-xCu复合钎料钎焊6061铝合金,研究了添加Cu元素和Al2O3颗粒对钎焊性能的影响。基于密度泛函理论(DFT)和GGA-PBE理论,对Al2O3 / Sn9Zn的界面结构,界面能,接触角和电子性能进行了第一性原理计算。计算表明,Sn9Zn-1Al2O3-4.5Cu和Sn9Zn-1Al2O3-6Cu具有稳定的结构,相应的结果如图6和7所示[10]。
图6.不同结构的具有不同电荷密度差的轮廓平面:(a)Sn9Zn-1Al2O3,(b)Sn9Zn-1Al2O3-4.5Cu
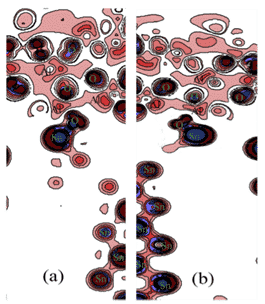
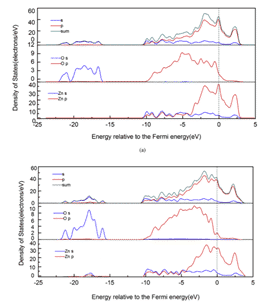
图7不同结构的局部态密度:(a)Sn9Zn-1Al2O3,(b)Sn9Zn-1Al2O3-4.5Cu
其他应用
例如,Kulwinder Kaur等人。使用密度泛函理论(DFT)和玻尔兹曼传递理论来研究fcc HfRhSb的高温热电性质。图8和图9显示了计算出的能带结构和状态密度,以及一些物理参数。传输特性的理论始于能带结构的计算,刚性带中的玻尔兹曼传输理论以及恒定弛豫时间近似(RTA)。刚性性能带近似(RBA)是研究带结构与热电响应之间关系的有效工具[11]。
图8(a)能带结构(b)完整的局部态密度(c)声子色散(d)声子DOS
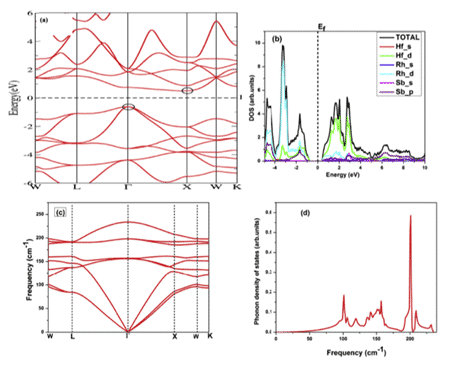
图9塞贝克系数,电导率,热导率和热电效率ZT与温度的关系

参考
1.Heisenberg W.运动学和力学关系的量子理论重新解释[J]。 Z Phys,1925,33:879
2.Schrodinger E,量子问题I [J]。 Ann der Phys,1926,9:361
3.Hohenberg P,Kohn W.不均匀电子气[J]。 B物理学报,1964,136(3):864
4.Kohn W,Sham L J.包括交换和相关效应的自洽方程[J]。物理学评论A,1965,140(4):1133
5.Leineweber,T。Hickel,B。Azimi-Manavi,SB Maisel,通过DFT计算分析Fe4C和Fe4N的晶体结构:探索了基于FCC的间隙上层结构[J],材料学报140(2017)433-442
6.李志林,夏春阳,张正平,窦梅玲,季静,宋烨,刘景军,王峰,化学计量失配组成的薄膜太阳能电池中钾钛矿Cu 2 ZnSnS 4的相稳定性第一性原理研究[J],化学学报,合金与化合物学报768(2018)644-651
7.Benkabou,H。Rached,A。Abdellaoui,D。Rached,R。Khenata,MH Elahmar,B。Abidri,N。Benkhettou,S。Bin-Omran,四元Heusler合金CoRhMnZ的电子结构和磁性(Z = Al,Ga,Ge和Si)的第一性原理计算[J],合金与化合物学报647(2015)276-286
8.宋慧金,顾鹏,朱兴华,闫强,杨定宇,基于第一性原理的TiN薄膜的电子结构和光学性质研究[J],物理B:凝聚态545(2018)197-202
9.黄硕,李晓青,何煌,埃里克·霍尔姆斯特罗姆,莱芬特·维托斯,第一性原理的FeCrCoMnAlx高熵合金的力学性能[J],材料化学与物理210(2018)37-42
10.余露,马乐,李树勇,左维,纪志强,丁敏,Cu元素添加对Sn9Zn-1Al2O3钎焊6061铝合金界面行为和力学性能的影响:第一性原理计算和实验研究[J],合金与化合物学报765(2018)128-139
11.Kulwinder Kaur,Ranjan Kumar,DP Rai,HfRhSb半Heusler化合物在高温下的有希望的热电响应:第一个原理研究[J],合金与化合物学报763(2018)1018-1023








