当构件的某一点受到足够大的扰动应力时,经过足够次数的循环后就会形成裂纹,这种现象称为疲劳。疲劳断裂是工程结构和构件失效的主要原因。目前的应用和研究中,疲劳测试方法主要有四类:
1、名义应力应变法;
2、局部应力应变法;
3、能量法;
4.断裂力学方法。
本文简要介绍了这四种方法及其应用。
1、名义应力法
名义应力法是对标准构件进行额定应力试验的方法,根据最大循环应力与屈服应力的关系分为应力疲劳和应变疲劳。
首先引入应力疲劳,如果最大循环应力Smax小于屈服应力Sy,则定义为应力疲劳。由于经应力疲劳试验,材料寿命达104次以上,因此应力疲劳又称为高周疲劳。根据应力疲劳理论,金属材料的应力S与失效循环次数N呈非线性分布。可用幂函数:取对数: ,或用指数:取对数来表示,这种方法称为SN法。实际测试中使用SN曲线或p(存活率)-SN曲线对结果进行分析。
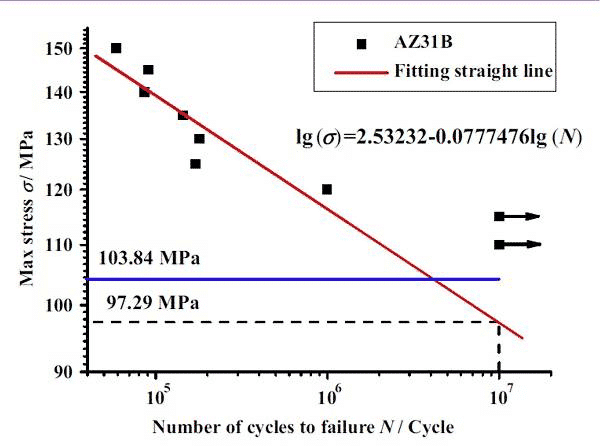
材料疲劳SN曲线一般采用应力疲劳。如图1和图2所示,采用提升法测试AZ31B镁合金的疲劳极限(应力比为0.1,疲劳寿命对应疲劳载荷为107)。图中AZ31B镁合金试样的疲劳极限为97.29 MPa。
图1 AZ31B镁合金疲劳试验

图2 AZ31B镁合金疲劳试验SN曲线
应变疲劳适用于高负载、低设计寿命部件的测试。定义为:如果最大循环应力Smax大于屈服应力Sy,则为应变疲劳。应力疲劳试验用于研究部件在高负载和低频下的情况。例如,压力容器在使用寿命期间,总循环次数为104次左右,因此采用应变作为疲劳性能参数描述。应力疲劳也称为低周疲劳。
学者们基于应变疲劳研究提出了以下理论,材料的应力应变(Remberg-Osgood弹塑性应力-应变)关系:
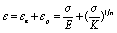
式中,εe为弹性应变幅,εp为塑性应变幅。
在等幅对称应变试验中,由于材料发生塑性变形,当应变减小时,应力不能按原来的路径减小,应力-应变曲线呈环形。这条曲线称为磁滞回线。随着循环次数的增加,同应变幅应力会增大或减小。这种应力对应于变化的响应称为循环硬化或循环软化。循环足够几个循环,有些材料会形成稳定的磁滞回线。
在应变疲劳中,应力-应变曲线用于描述材料的循环硬化或循环软化趋势。对于具有对称磁滞回线曲线的材料,称为 Massing 材料。
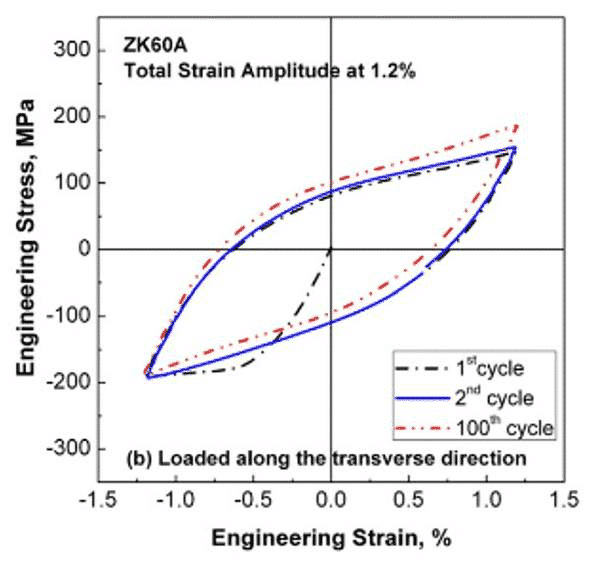
下图为ZK60镁合金在轧制方向和横向加载时的σ-ε曲线。在横向上,循环硬化现象明显。
图3 ZK60A镁合金轧制载荷沿σ-ε曲线
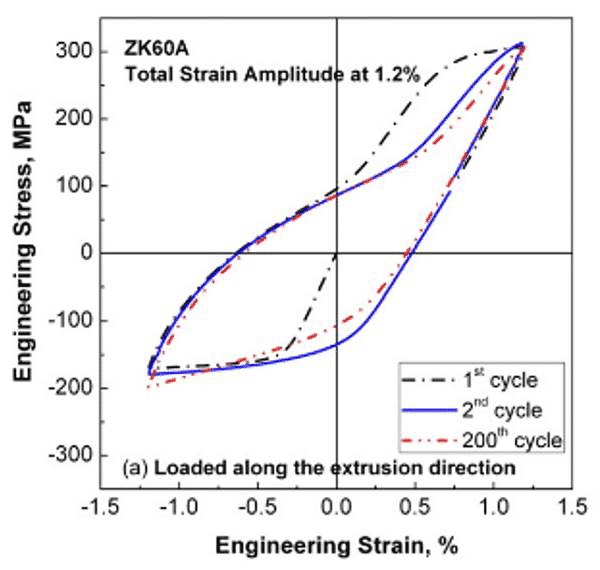
图4 ZK60A镁合金载荷沿横向σ-ε曲线
2. 局部应力应变法
对于缺口试样和应力集中部件,采用局部应力应变分析。目前的研究表明,构件的疲劳寿命是局部最大应变和应力,并提出了应力集中因子的概念。适用于计算材料裂纹形成的寿命和预测构件的残余疲劳寿命。
局部应力法提出的理论有Neuber公式(应力集中公式)
明纳理论(疲劳累积损伤理论):构件在恒定应力S下的疲劳寿命为N,则经过n次循环的损伤为:
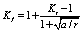
如果在 k 个恒定应力 Si 下进行 ni 个循环,则总损伤可定义为:
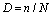
损坏标准是:
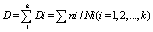
局部应力法的应用如图5和图6所示。
图 5. 缺口试样的疲劳寿命预测
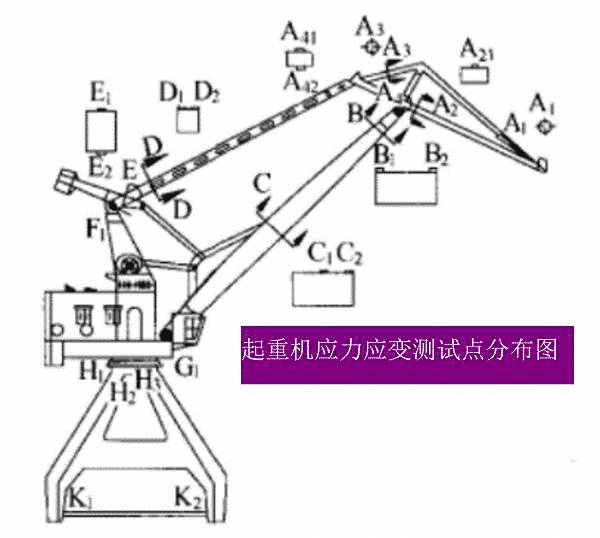
图6 起重机疲劳寿命预测(起重机应力应变测试点分布图)
应力集中点疲劳寿命按下式计算:
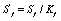
式中:Sf——等效应力光滑样品疲劳寿命
图6 起重机疲劳寿命计算方法是输入不同试验点的时程图并输入各点的疲劳寿命方程,计算各点的残余疲劳寿命。默认寿命最小点是设备的剩余疲劳寿命。对于起重机,学者建议普通钢材的累积损伤值D达到0.68。
3.能量法
红外热成像是一种基于材料疲劳过程能量常数定律预测疲劳性能的方法。疲劳热成像方法是基于疲劳过程中的热力学能U、动能K以及其他形式的能量耗散。物体吸收或耗散的能量变化E和热变化Q之和应为作用在物体上的功W。相同。
疲劳热成像具有无损、实时、非接触的优点。同时,由于能量耗散与疲劳载荷之间的非线性关系,以及利用散热进行温度耗散的误差,仍不适合工业测量。
目前研究提出了以下预测模型理论、Luong方法、ΔTmax和疲劳寿命Nf如下:
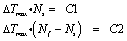
其中:C1、C2为常数。
因此,可以通过两线法来预测疲劳极限。基于散热,学者们提出了以下模型:
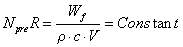
R-温升斜率
以下是太原理工大学张红霞老师团队对疲劳热成像方法的研究。通过热成像快速预测AZ31B镁合金的疲劳寿命。只需测试样品第一阶段的温升即可根据两线法预测材料的疲劳极限。分别如图7、图8、图9。
图7 AZ31B镁合金疲劳试验不同循环次数的表面温度
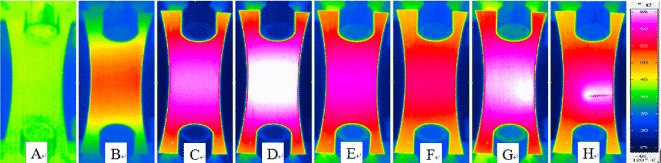
图8 AZ31B疲劳过程样品表面温度曲线
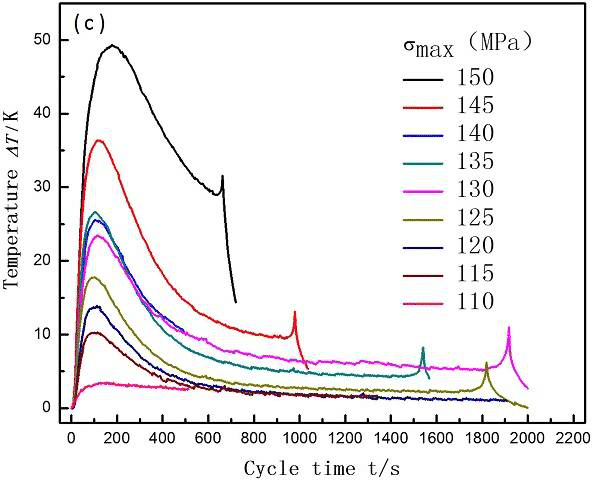
图9 温度随疲劳载荷的变化
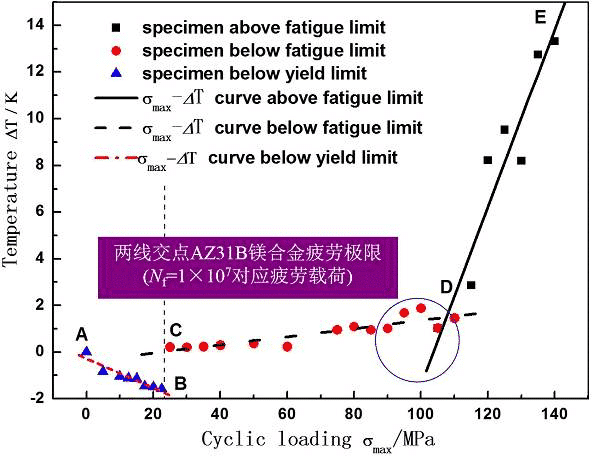
4 断裂力学方法
线弹性断裂力学是研究疲劳裂纹扩展的理论基础。疲劳裂纹扩展也可以用应力强度因子K来定量描述。
在疲劳载荷作用下,裂纹长度a随循环次数N的变化率,da/dN,即为疲劳裂纹扩展速率,反映裂纹扩展的速度。对于给定的裂纹长度 a,da/dN 随着循环应力幅值 Δσ 的增加而增加(Δσ 越大,ΔK 越大)。基于这一现象,学者们研究了da/dN-ΔK(裂纹扩展)。速率-应力强度增加曲线,曲线可分为三个区域:低速率区、中速率区、高速率区。巴黎公式指出,中等利率的稳定延伸之间存在线性关系:
裂纹尖端形状的经验公式:
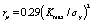
疲劳裂纹的形成和扩展可以统一在损伤力学的框架下。
下面对AZ31B镁合金的裂纹扩展速率进行研究,并对AZ31B的稳定扩展速率进行评价。
图10 疲劳裂纹尖端竞争机制示意图
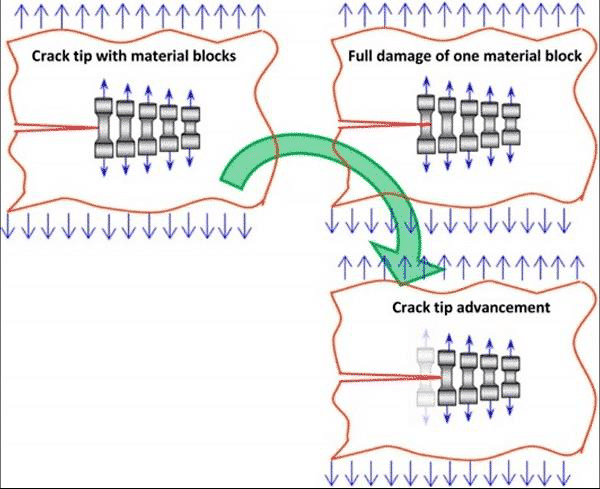
图11 裂纹尖端应力应变场三个不同区域示意图
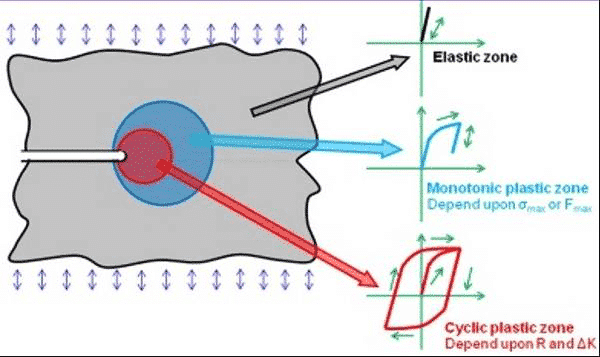
图12 疲劳裂纹尖端竞争机制aN曲线示意图
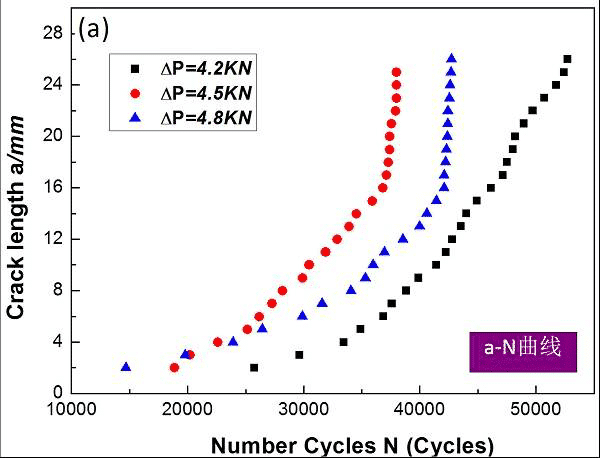
图13 疲劳裂纹尖端竞争机制da/dN-ΔK曲线示意图
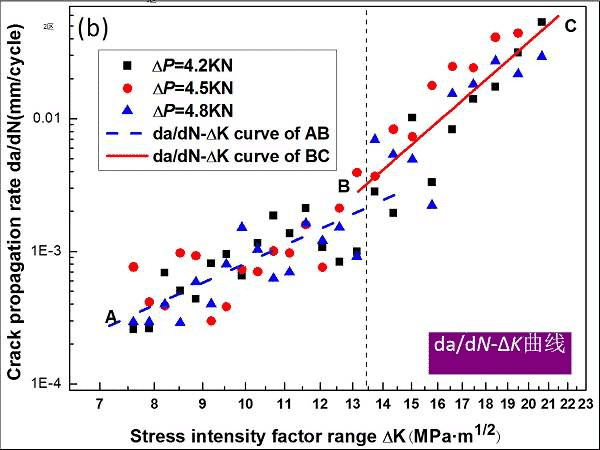
AB段(中速区):da/dN=4.57×10-7(ΔK)3.25 (7.2<ΔK≤13.5 MPa•m1/2)
BC段(高速率区):da/dN=3.16×10-10(ΔK)6.21(13.5<ΔK≤22.1 MPa•m1/2)
结论:
这四种方法在应用上有所不同。名义应力法和局部应力法适用于工业领域的材料和构件性能测试。能量法可以预测材料的疲劳寿命,断裂力学方法成功地将疲劳裂纹的形成和扩展统一起来。








