为了使微观模拟系统能够反映宏观的实验现象,需要通过周期性边界条件对模拟对象系统进行周期性复制,以避免实际中不存在的边缘效应。原则上,任何分子系统的理论研究都需要求解随时间变化的薛定谔方程。然而,在实践中,更多地关注原子核的轨迹。这样的轨迹可以通过使用 Born-Oppenheimer 近似求解经典的机械运动方程来获得。奥尔德和温赖特曾表示,计算机模拟实验将成为连接宏观实验现象和微观自然的重要桥梁。经过 10 年的首次分子动力学模拟实验,法国物理学家 Verlet 提出了牛顿运动方程的积分算法。同时,提出了另一套生成和记录相邻原子对的算法,大大简化了原子间相互作用的计算。这两种算法在一些变体中仍然被广泛使用 [1, 2]。
在过去的几十年中,已经开发了多种原子级模拟方法,包括晶格静力学、晶格动力学、蒙特卡罗和分子动力学。其中,分子动力学特别适用于塑性变形的研究。它通过求解一些定义的原子间相互作用势函数的原子相互作用系统的牛顿方程来研究变形过程的实时行为,并包括晶格的非化简。系统的谐波、内应力高度不均匀和瞬态响应。
分子动力学主要依靠牛顿力学来模拟分子系统的运动,以从由分子系统不同状态组成的系统中提取样品,从而计算出系统的构型积分,并根据构型结果进一步计算系统积分。热力学量和其他宏观性质。它解决了由核和电子组成的多体系统的运动方程。它是一种可以解决大量原子组成的系统动力学问题的计算方法。它不仅可以直接模拟物质的宏观演化特征,而且可以与测试结果相吻合。类似的计算还可以提供微观结构,粒子运动及其与宏观特性的关系的清晰图像,为新理论和新概念的开发提供有力的技术支持。
分子动力学的目的是一个粒子系统。系统中原子之间的相互作用由势能函数描述。因此,正确选择势函数的类型及其参数在仿真结果中起着重要作用。在大多数情况下,势能函数简化了分子几何变形的描述,以至仅使用简单的谐波项和三角函数的程度。代替键原子之间的相互作用,仅使用库仑相互作用和伦纳德-琼斯势能。结合来描述。其中,原子间相互作用力的描述通常是经验性的或半经验性的,可以提高计算效率,但不能充分揭示电子键的多体性质,特别是与其结构和化学性质有关的复杂性。缺陷附近。自洽变函数。 Daw和Baskws的EAM(嵌入原子模型)势能在某种程度上结合了电子键合的多体特性。
势函数的可靠性主要取决于力场参数的准确性,并且可以通过拟合实验观察数据和量子力学从头算数据来获得力场参数。目前,在生物大分子系统的模拟中使用最广泛的分子力场是CHARMM力场和AMBER力场,这是对生物大分子进行早期研究的分子力场。现有的力场参数仍在不断优化,所覆盖分子的类型也在不断扩大。粗粒度模型在计算生物物理研究中越来越受到关注,因为在此模型中定义了粗粒状颗粒,对应于全原子模型中的几个原子或原子团甚至分子。系统中的粒子数量减少了,因此可以大大改善模拟的时间和空间尺度,但是原子的细节也会丢失。基于此模型的分子动力学模拟适用于研究缓慢的生物现象或依赖大型装配体的生物现象。
设计基本力场的基本原理是在一个时间步中最小化计算能量开销以最大化仿真范围。这对于完整的原子力场尤其重要,即使对于所谓的粗粒度模型也是如此。特别是,如果您要模拟微秒或什至毫秒的时间标度,则此原理非常重要。
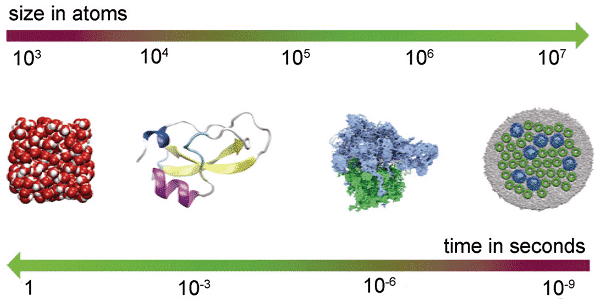
图1从左到右显示了分子动力学的时空维度之间的反比关系:(1)水,细胞的基本组成; (2)牛胰蛋白酶抑制剂,一种酶,“可以在毫秒级别检查呼吸行为;(3)核糖体,可以解码遗传信息并产生蛋白质的复杂生物装置;(4)紫色细菌光合膜碎片,图中有2500万个原子,该图显示了嵌入在磷脂双层和光化学反应中心中的光捕获络合物。
图1经典分子动力学的时空尺度关系
随着计算机处理器的快速增长和大规模并行计算体系结构的发展,大规模并行化或专有体系结构技术与可扩展的分子动力学程序的结合,计算机模拟的范围从位错到基于晶粒边界的变形机制。整个晶粒尺寸范围为探索材料系统的研究前沿开辟了新途径。
例如,威廉·贡萨尔维斯(WilliamGonçalves)等。使用大型原子/分子平行模拟器LAMMPS(大型原子/分子大规模平行),使用Wolf BKS(van Beest,Kramer和van Santen)势函数来描述原子之间的相互作用。 Simulator)研究了二氧化硅气凝胶的弹性和强度的分子动力学。他们使用了速度Verlet算法和1.0 fs的时间步长,并在所有三个方向上使用了周期性边界条件。
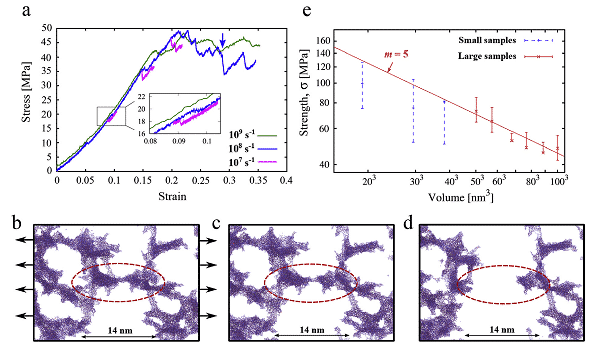
图2是超过7,000,000个原子的模拟大体积样品的3D示意图,还有20 nm厚的样品截面和局部放大图(蓝色是氧原子,红色是硅原子),图3(a )是803 nm 3气凝胶。对样品进行单轴拉伸测试,以获得300 K的应力-应变曲线,(bd)是典型的韧性断裂图像,并且(e)抗拉强度与样品体积之间的对数关系。他们分析说,为了确保正确评估机械性能(例如弹性),模拟样品的大小至少是孔径的8倍,而具有正表面高度的二氧化硅气凝胶则要求相对较低的应变率以确保准静态条件。
图2模拟的二氧化硅气凝胶样品(超过700万个原子)
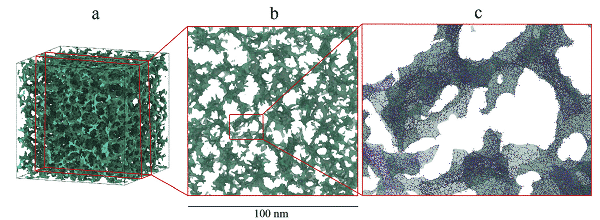
图3单轴拉伸试验的应力-应变曲线(a),强度-体积关系(e)和断裂图像(bd)
通常,临界晶粒尺寸dc约为20-30 nm,较大的晶粒尺寸(50-100 nm)变形主要是由位错决定的。当晶粒尺寸小于30nm时,其主要由GB变形过程主导,并且晶粒尺寸减小。这导致强度和流动应力降低,即“抗霍尔效应”。但是,用于模拟fcc和bcc金属中GB的多体和成对电位之间的广泛比较表明,通过这些不同的力描述所预测的行为在质量上几乎没有差异,这表明多体效应可能不会主导GB行为。
Bejaud,J。Durinck等。利用分子动力学模拟研究了变形孪晶与纳米结构Cu / Ag界面之间的相互作用,分析了界面结构对孪晶形核,膨胀和增稠的影响,并解释了失配界面。错位网格的作用。图4显示了Shockley部分位错网格(用黑线突出显示),三角形图案(白色部分)以及界面处的堆垛层错分布。其中,原子根据中心对称性参数着色,蓝色原子处于理想的FCC环境中,红色原子处于堆积缺陷或孪生缺陷中。
图4(a)沿界面的Cu和Ag原子的俯视图:(ai)COC界面,(a.ii)TO界面,(b)沿X = <011>方向的侧视图:(bi)在COC中在界面和壳体之间,相干区域与固有堆垛层错(ISF)区域交替出现(b.ii)TO界面,并且双缺陷区域连续存在于Cu层和Ag层中。
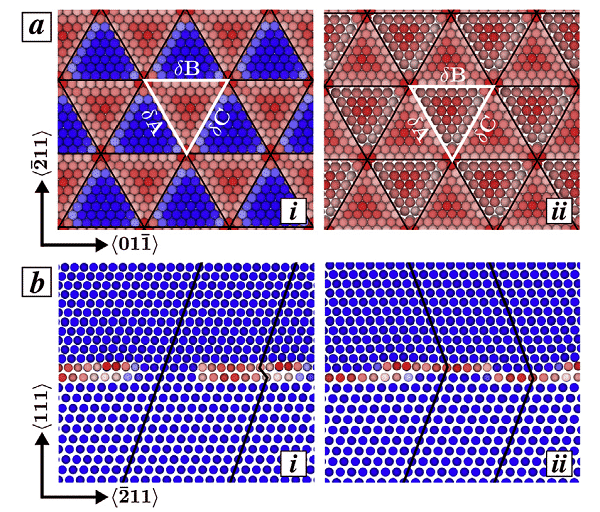
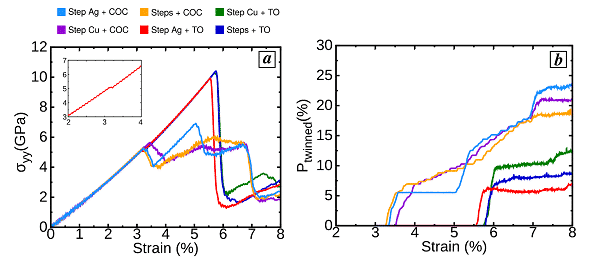
图5显示了应力-应变曲线和孪晶的原子比与应变的关系。通过分析,他们发现界面可以通过Lomer位错直接或间接诱导孪晶位错成核,并且异质界面结构如何影响机械孪晶过程的不同步骤,从而影响钽在纳米结构Cu / Ag中的形成。晶体的大小。这种原子级方法为纳米级复合材料的机械孪生过程提供了一些有用的理论基础。
图5(a)应力-应变曲线,(b)孪晶的原子比与应变的关系
在控制变形机理的同时,设计多层材料来调节机械性能是一个热门话题,因为孪晶允许纳入纳米层和纳米晶体材料的机械性能。在这方面,本研究为理解双界面相互作用的机理提供了关键,并支持异相界面促进孪生的观点。
对于含有低对称性hcp结构金属的超精细层状复合材料,大量异质界面可以有效吸收核辐照引起的空位和间隙原子等缺陷,而且hcp金属本身密度、比强度和,由Ti、Zr、Mg等金属组成的六方多层材料,由于具有较高的比刚度和良好的导电导热性,开始受到人们的关注。但与晶体结构对称性高的fcc和bcc金属相比,hcp金属的室温塑性变形能力较差,限制了相关复合材料的使用。
除了原子尺度的时空分辨率外,分子动力学模拟还可以描述完全表征的理想化纳米晶体模型的行为,例如界面结构,驱动力和原子机理。另一方面,它可以处于非常高的晶界和位置。在错误的密度下观察到较大的塑性变形行为。例如,位错成核机理,晶界淬火,纳米晶Al中的机械孪生,晶粒尺寸从位错减小到基于晶界的变形机理,剪切带及其断裂表面关系的观察。
此外,在实际应用和研究过程中,针对不同问题的描述和选择的理论模型,动力学已经发展出许多理论分支,例如宾夕法尼亚大学的简汉,斯宾塞·托马斯等边界的力量断层的描述总结了多晶材料的晶界动力学概念,Zheng Ma等。研究了FeCO3的沉淀动力学以及表面/界面动力学。







