El método de cálculo analógico comúnmente utilizado en el campo del litio.

En las últimas décadas, las baterías de iones de litio han llamado la atención en el campo de los materiales energéticos. Al mismo tiempo, con el desarrollo de la teoría básica y el campo informático, se han aplicado muchos métodos de simulación computacional en la investigación de baterías de iones de litio. Debido a errores en el proceso experimental, escalas microscópicas, como el mecanismo de crecimiento de las membranas SEI, la dinámica de difusión de iones en los materiales de los electrodos, la evolución de las estructuras durante la carga y descarga de los materiales de los electrodos, la relación entre el potencial y la estructura, y la La distribución de las capas de carga espacial no se puede resolver. Conclusiones intuitivas, los métodos experimentales no pueden dar una explicación teórica clara. En contraste, los métodos de simulación computacional tienen ventajas relativas para comprender la evolución de la química interna y la electroquímica de las baterías de iones de litio. Los cálculos teóricos verifican los resultados experimentales de los materiales de la batería de iones de litio, y también promueven y guían el desarrollo de los materiales de la batería. A continuación presentamos varios métodos de cálculo analógico de uso común y sus aplicaciones en baterías de iones de litio.

La teoría funcional de la densidad se ha utilizado ampliamente en la investigación de baterías de iones de litio. Se usa comúnmente para calcular la estabilidad estructural, el potencial de inserción de litio, la estructura electrónica, la banda de energía, la estructura de relajación, la energía de generación de defectos, la ruta de migración, la energía de activación y el litio. Propiedades como la cinética del transporte de iones y la desintercalación de las transiciones de fase de litio.

El valor de voltaje de la batería es un parámetro asociado con un cambio en la energía libre de la reacción de la batería. Los diferentes materiales tienen un potencial de inserción de litio inherente. Idealmente, el material del electrodo tiene un potencial más alto para el electrodo positivo, un potencial más bajo para el electrodo negativo y una diferencia de potencial entre los diferentes electrodos. La potencia de la batería de iones de litio se puede calcular de acuerdo con la respuesta de la batería: (la potencia de 1 mol de electrones se expresa por F, y la potencia de un electrón es

1.602 × 10−19 C) F = NA · e− = 96487.56 C / mol

Sea n el número de cargas transferidas durante la reacción de la batería, luego la batería a través de la batería es nF, el trabajo eléctrico máximo realizado por la batería es:

−Wr'=nFVAVE

Bajo condiciones isostáticas isotérmicas, la energía libre de Gibbs del sistema es igual al trabajo realizado por el sistema para el mundo exterior:

ΔG=−Wr'

ΔG = nFVAVE ， Y debido a que Li + tiene una unidad de carga, VAVE = ΔG / F

ΔG es la energía libre de Gibbs de la reacción de la batería, suponiendo que el cambio en el volumen y la entropía causados por la reacción de incrustación celular es insignificante, entonces

ΔG≈ΔE

entonces: VAVE = ΔE / F

Para un sistema de batería en el que el electrodo positivo es LiA y el electrodo negativo es B, se supone que x litio se elimina de LiA y se incrusta en B después de la carga (proceso de carga positiva), y la fórmula de reacción es:

LiA + B → Li1 − xA + LixB

El voltaje promedio de este proceso es la diferencia entre la energía de cada estado final correspondiente de litio (Li1 − xA, LixB) y el estado inicial (LiA, B), luego el voltaje:

V = [E (Li1 − xA) + E (LixB) −E (LiA) −E (B)] / xe

Cuando el electrodo negativo es litio metálico, se puede simplificar como:

V = [E (Li1 − xA) + E (Lix) −E (LiA)] / xe

Al calcular la energía total de cada sustancia antes y después de la reacción, el potencial del electrodo se puede calcular de acuerdo con la fórmula anterior. Sin embargo, para casi todos los materiales catódicos, el voltaje calculado por la teoría funcional de la densidad es bajo. Al aplicar una corrección + U al GGA estándar, es decir, al método GGA + U, o al usar el HSE06 funcional híbrido, se puede obtener un voltaje más cercano al valor experimental. En el cálculo de los materiales de cátodos de óxido que contienen iones de metales de transición 3d, el fuerte efecto de correlación se ha reconocido como un efecto a considerar.

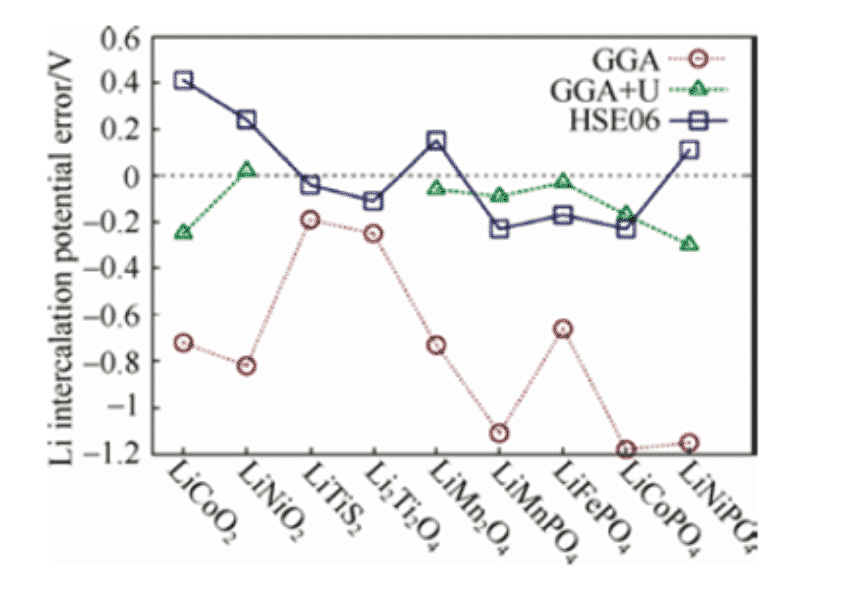
Figura 1: GGA estándar y GGA + U, HSE06 Calcular varios iones de litio

El cálculo de los primeros principios basado en la densidad funcional puede obtener las propiedades del material en el estado fundamental de temperatura cero. El transporte de átomos e iones en el material puede estudiarse mediante simulación de dinámica molecular a temperatura finita. El cálculo de la dinámica molecular se utiliza como un método de simulación a nivel atómico que utiliza la función de potencial empírico. En comparación con el método de los primeros principios, puede realizar una simulación a mayor escala, que puede mostrar mejor el proceso de difusión dinámica de iones de litio y analizarlo.

La dinámica molecular puede simular la evolución de las partículas del sistema a lo largo del tiempo, observar el camino de la migración de iones, calcular el coeficiente de difusión de las partículas y la estabilidad de los materiales, pero la ley del movimiento de partículas es la mecánica newtoniana y la existencia de partículas de baja calidad. como el hidrógeno y el helio El efecto de cálculo del efecto cuántico no es ideal. En términos de baterías de iones de litio, la dinámica molecular puede obtener el coeficiente de difusión y la ruta de migración de los iones en los materiales, lo que nos brinda la posibilidad de comprender el mecanismo de difusión de los iones en los materiales.

Yang calculó el proceso de autodifusión de LiFePO4 y descubrió que la migración de Li + en el material no ocurre continuamente, sino que ocurre a través de la transición entre las posiciones de red adyacentes. En 2014, Zhang Jungan y otros de la Universidad de Shanghai utilizaron la dinámica molecular para simular el comportamiento de difusión de los iones de litio entre las capas de grafito durante la carga. Se estudiaron las propiedades de difusión de iones de litio de los materiales de ánodo de grafito a 300 K. Los resultados experimentales proporcionan datos básicos para el estudio del modelo a escala continua de la deformación del electrodo de la batería de iones de litio.

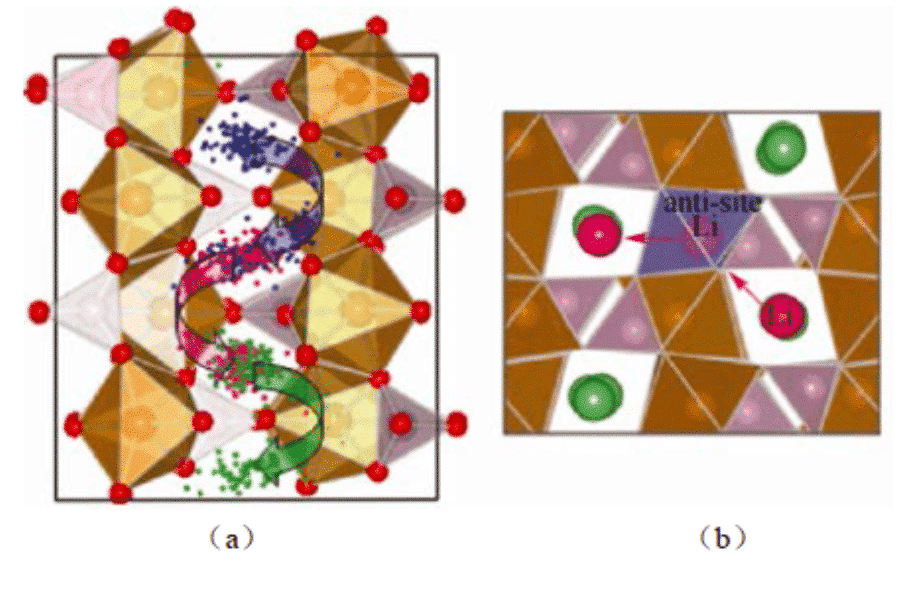
Figura 2: La simulación de dinámica molecular muestra (a) la trayectoria de los iones Li en LiFePO4; (b) la migración de iones de Li entre los canales a través de defectos de ocupación mutua de Li / Fe

El método de campo de fase se basa en la teoría de Ginzburg-Landau. La ecuación diferencial se usa para representar la difusión, el potencial de ordenamiento y el impulso termodinámico de un mecanismo físico específico. Las ecuaciones anteriores se resuelven mediante programación informática. Estudie el estado instantáneo del sistema en el tiempo y el espacio. El modelo de campo de fase se basa en los principios fundamentales de la termodinámica y la dinámica y es una herramienta poderosa para predecir la evolución de las microestructuras durante las transiciones de fase de estado sólido.

El modelo de campo de fase puede simular el crecimiento de cristales, la transformación de fase sólida, la evolución de grietas, la transición de fase de película, la migración de iones en la interfaz, etc., pero los resultados de la simulación son la falta de comparación cuantitativa con la observación del tiempo. El grosor de la interfaz generalmente se establece más grande que la situación real. , lo que lleva a la falta de detalles. Marnix Wagemaker (autor correspondiente) de la Universidad Tecnológica de Delft en los Países Bajos publicó un artículo en la revista Adv.Funct.Mater. en 2018 para proponer un modelo de campo de fase termodinámica para la inserción de iones de litio en la espinela Li4Ti5O12, integrando datos DFT. La capacidad de describir el comportamiento termodinámico completo de las partículas separadas por fases proporciona una dirección específica para diseñar el electrodo Li4Ti5O12 de mejor rendimiento.

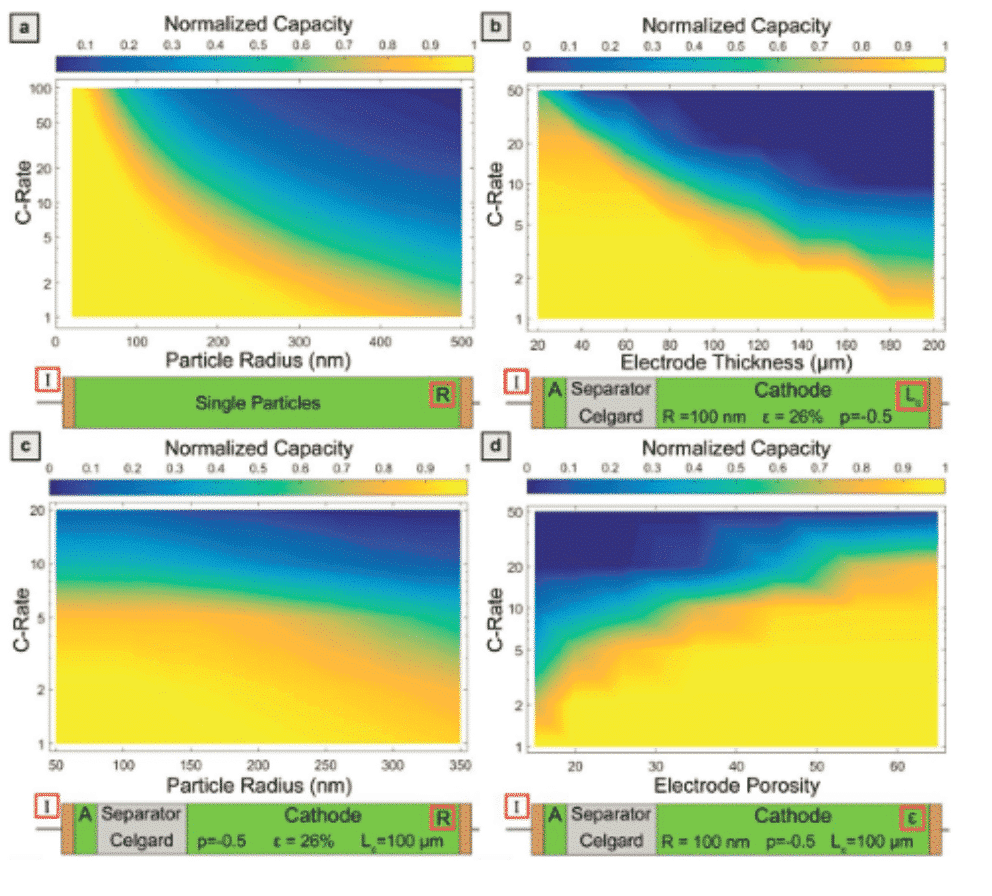
Figura 3: simulación de partículas individuales LTO, la relación entre la capacidad de la batería y la capacidad de descarga nominal y el grosor del electrodo bajo simulación de electrodo poroso

El método de elementos finitos es una técnica numérica para resolver la solución aproximada del problema del valor límite de las ecuaciones diferenciales parciales. El flujo de la simulación del método de elementos finitos es el siguiente: 1. Discretización del área del problema de solución 2. Determine la variable de estado y el método de control variable de la región, es decir, la ecuación de evolución del espacio de tiempo variable; 3. Derive la unidad individual, ensamble la unidad. La solución general se resuelve, y finalmente se resuelven las ecuaciones simultáneas y se obtienen los resultados.

Para comprender mejor el comportamiento de sobrecalentamiento de las baterías de iones de litio de gran capacidad y alta potencia para vehículos eléctricos, Cao Binggang de la Universidad Xi'an Jiaotong utilizó el método de elementos finitos para simular la temperatura interna de la batería durante la consideración de la resistencia interna. convección y disipación externa. La distribución espacial, los resultados de simulación de distribución de temperatura de la celda de prueba en un horno caliente a 155 °C y la composición de la batería de VLP50/62/100S-Fe (3,2 V/55 A·h) LiFePO4/grafito.

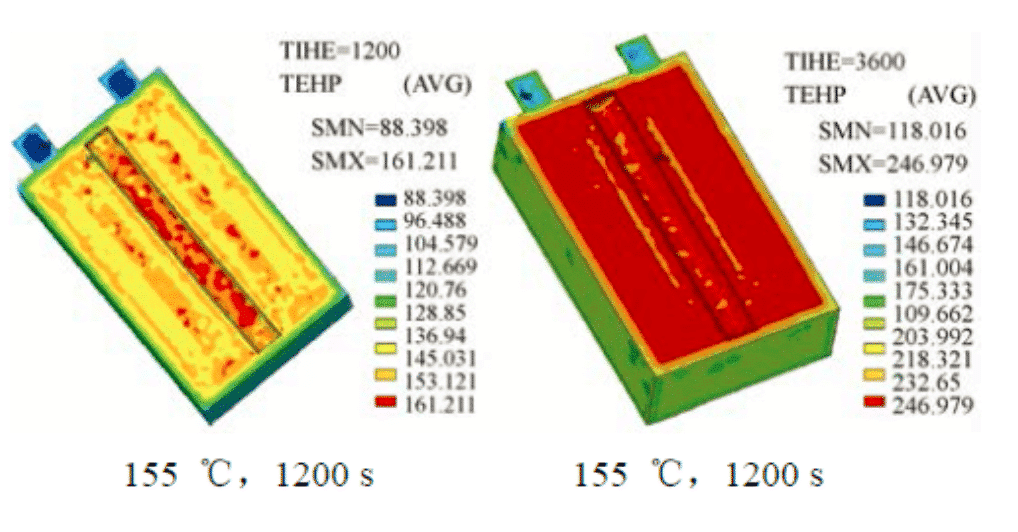
Figura 4: Distribución de simulaciones de elementos finitos en la celda a 155 ° C, 1200 sy 3600 s

Las simulaciones de materiales macroscópicos, como los modelos de campo de fase y los métodos de elementos finitos, se centran en cuestiones de ingeniería y ayudan a comprender fenómenos macroscópicos como el estrés, la transferencia de calor, el flujo y el acoplamiento multicampo en baterías de iones de litio. El cálculo de los primeros principios basado en la teoría funcional de la densidad es más propicio para las propiedades microfísicas, como la energía y la estructura electrónica del sistema de materiales.

Con el desarrollo de la teoría y la amplia aplicación de la simulación por computadora, la ciencia de los materiales computacionales dirigirá y verificará la ciencia de los materiales experimentales. El cálculo de la escala macroscópica a la teoría microscópica promoverá en gran medida el desarrollo del campo de materiales, para baterías de iones de litio. En términos de los muchos problemas en la ciencia experimental, con la ayuda de simulaciones computacionales, también será una explicación teórica clara. La comprensión de los métodos de simulación computacional para baterías de iones de litio acelerará el desarrollo y la aplicación de materiales de baterías de iones de litio.

Referencia:

[1] Huang Jie, Ling Shigang, Wang Xuelong, et al. Problema de ciencia básica de la batería de iones de litio (XIV) —— Método de cálculo [J]. Energy Storage Science and Technology, 2015, 4 (2): 215-230.

[2] Ji Xiang, Song Yicheng, Zhang Jungan. Simulación de dinámica molecular de las propiedades de difusión de Li_xC_6 en baterías de iones de litio [J]. Revista de la Universidad de Shanghai (Ciencias Naturales), 2014 (1): 68-74.

[3] Shi Siqi (Sisi Qi). Estudio de primeros principios de materiales catódicos para baterías de iones de litio [D]. Beijing: Instituto de Física Academia de Ciencias de China, 2004. [4] Yang JJ, Tse J S. Li mecanismos de difusión de iones en LiFePO4: Un estudio de dinámica molecular abinitio [J]. J. Phys. Chem A ， 2011，115 （45） ： 13045-13049.

[5] Vasileiadis A, Klerk NJJD, Smith RB, y col. Hacia un rendimiento óptimo y una comprensión en profundidad de los electrodos Spinel Li4Ti5O12 a través del modelado de campo de fase [J]. Materiales funcionales avanzados, 2018.

[6] Herzmann C, Günther G, Eker B y col. Modelado tridimensional de elementos finitos térmicos de baterías de iones de litio en aplicaciones de abuso térmico [J]. Journal of Power Sources, 2010, 195 (8): 2393-2398.