최근 수십 년 동안 리튬-이온 배터리는 에너지 재료 분야에서 주목을 받고있다. 동시에 기본 이론과 컴퓨터 분야의 발전과 함께 많은 계산 시뮬레이션 방법이 리튬 이온 배터리 연구에 적용되었습니다. 실험 과정의 오류로 인해 SEI 막의 성장 메커니즘, 전극 재료의 이온 확산 역학, 전극 재료의 충전 및 방전 중 구조의 진화, 전위와 구조의 관계 및 공간 전하 층의 분포는 해결 될 수 없다. 직관적 인 결론, 실험 방법은 명확한 이론적 설명을 제공 할 수 없습니다. 대조적으로, 전산 시뮬레이션 방법은 리튬-이온 배터리의 내부 화학 및 전기 화학의 진화를 이해하는데있어서 상대적 이점을 갖는다. 이론적 계산은 리튬 이온 배터리 재료의 실험 결과를 검증하고 배터리 재료의 개발을 촉진하고 안내합니다. 아래에서는 일반적으로 사용되는 몇 가지 아날로그 계산 방법과 리튬 이온 배터리에서의 응용 방법을 소개합니다.
밀도 기능 이론의 적용
밀도 기능 이론은 리튬 이온 배터리 연구에서 널리 사용되었습니다. 일반적으로 구조적 안정성, 리튬 삽입 전위, 전자 구조, 에너지 밴드, 이완 구조, 결함 생성 에너지, 이동 경로, 활성화 에너지 및 리튬을 계산하는 데 사용됩니다. 이온 수송 동역학 및 리튬 상 전이의 디 인터 칼 레이션과 같은 특성.
배터리의 전압 값은 배터리 반응의 자유 에너지의 변화와 관련된 파라미터이다. 다른 재료에는 고유 한 리튬 삽입 전위가 있습니다. 전극 재료는 이상적으로는 양극에 대한 높은 전위, 음극에 대한 낮은 전위 및 상이한 전극 사이의 전위차를 갖는다. 리튬 이온 배터리 전력은 배터리 응답에 따라 계산할 수 있습니다. (1 mol 전자 전력은 F로 표시되고 전자 전자 전력은
1.602 × 10-19 C) F = NA · e- = 96487.56 C / mol
n은 배터리 반응 중 전송 된 전하의 수이고, 배터리를 통한 배터리는 nF이며, 배터리에 의해 수행되는 최대 전기 작업은 다음과 같습니다.
-Wr'=nFVAVE
등온 등방성 조건에서 시스템의 깁스 자유 에너지는 시스템이 외부 세계에서 수행하는 작업과 같습니다.
ΔG=−Wr'
ΔG = nFVAVE , Li +에는 충전 단위가 있으므로 VAVE = ΔG / F
ΔG는 전지 삽입 반응에 의해 야기 된 부피 및 엔트로피의 변화가 무시할 수 있다고 가정 할 때, 전지 반응의 깁스 자유 에너지이다.
ΔG≈ΔE
그래서 : VAVE = ΔE / F
양극이 LiA이고 음극이 B 인 배터리 시스템의 경우, 충전 후 x 리튬이 LiA로부터 제거되고 B에 매립 된 것으로 가정하고 (양의 충전 공정), 반응식은 다음과 같다 :
LiA + B → Li1-xA + LixB
이 공정의 평균 전압은 각 리튬 대응 종료 상태 (Li1-xA, LixB)의 에너지와 초기 상태 (LiA, B)의 에너지와 다음의 전압의 차이입니다.
V = [E (Li1-xA) + E (LixB) -E (LiA) -E (B)] / xe
음극이 금속 리튬 인 경우 다음과 같이 단순화 할 수 있습니다.
V = [E (Li1-xA) + E (Lix) -E (LiA)] / xe
반응 전 및 후에 각 물질의 총 에너지를 계산함으로써, 전극 포텐셜은 상기 식에 따라 계산 될 수있다. 그러나 거의 모든 음극 재료의 경우 밀도 기능 이론으로 계산 된 전압이 낮습니다. 표준 GGA, 즉 GGA + U 방법에 + U 보정을 적용하거나 하이브리드 기능 HSE06을 사용하여 실험 값에 가까운 전압을 얻을 수 있습니다. 3 차원 전이 금속 이온을 함유하는 산화물 캐소드 물질의 계산에서, 강한 상관 효과는 고려 될 효과로 인식되어왔다.
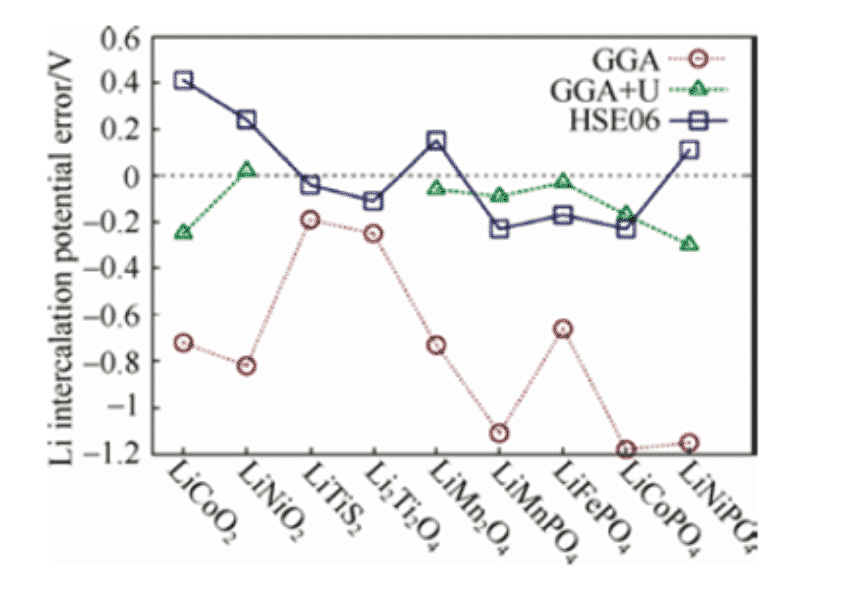
그림 1 : 표준 GGA 및 GGA + U, HSE06 다양한 리튬 이온 계산
분자 역학 방법
밀도 기능에 기초한 1 차 원리 계산은 영하 온도의 접지 상태에서 재료의 특성을 얻을 수 있습니다. 재료에서 원자와 이온의 수송은 유한 온도에서의 분자 역학 시뮬레이션에 의해 연구 될 수 있습니다. 분자 역학 계산은 경험적 전위 함수를 사용하는 원자 수준 시뮬레이션 방법으로 사용됩니다. 첫 번째 원리와 비교할 때 리튬 이온 동적 확산 프로세스를 더 잘 표시하고 분석 할 수있는 대규모 시뮬레이션을 수행 할 수 있습니다.
분자 역학은 시간이 지남에 따라 시스템 입자의 진화를 시뮬레이션하고, 이온 이동 경로를보고, 입자의 확산 계수와 재료의 안정성을 계산할 수 있지만, 입자 운동의 법칙은 뉴턴 역학이며 저품질 입자의 존재 수소 및 헬륨과 같은 양자 효과 계산 효과는 이상적이지 않습니다. 리튬-이온 배터리와 관련하여 분자 역학은 물질에서 이온의 확산 계수와 이동 경로를 얻을 수 있으며, 이는 물질에서 이온의 확산 메커니즘을 이해할 수있는 가능성을 제공합니다.
Yang은 LiFePO4의 자기 확산 과정을 계산하여 재료에서 Li +의 이동이 지속적으로 발생하지 않지만 인접한 격자 위치 사이의 전이를 통해 발생한다는 것을 발견했습니다. 2014 년 상하이 대학의 Zhang Jungan과 다른 사람들은 분자 역학을 사용하여 충전 중에 흑연 층 사이의 리튬 이온의 확산 거동을 시뮬레이션했습니다. 300K에서 흑연 애노드 물질의 리튬 이온 확산 특성을 연구 하였다. 실험 결과는 리튬 이온 배터리 전극 변형의 연속 스케일 모델 연구에 대한 기본 데이터를 제공합니다.
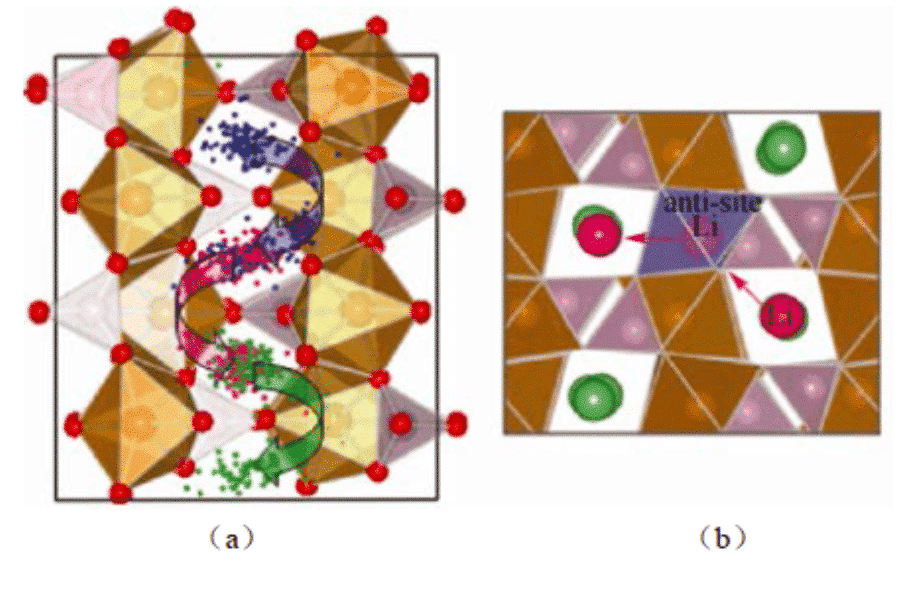
그림 2 : 분자 역학 시뮬레이션은 (a) LiFePO4에서 Li 이온의 궤적; (b) Li / Fe 상호 점유 결함을 통한 채널 간 리튬 이온의 이동
위상 필드 모델
위상 필드 방법은 Ginzburg-Landau 이론을 기반으로합니다. 미분 방정식은 특정 물리적 메커니즘의 확산, 순서 및 열역학적 구동을 나타내는 데 사용됩니다. 위의 방정식은 컴퓨터 프로그래밍으로 해결됩니다. 시간과 공간에서 시스템의 순간 상태를 연구하십시오. 위상 필드 모델은 열역학 및 역학의 기본 원리를 기반으로하며 고체 상태 전이 동안 미세 구조의 진화를 예측하는 강력한 도구입니다.
위 상장 모델은 결정 성장, 고체상 변환, 균열 진화, 막 위상 전이, 계면에서의 이온 이동 등을 시뮬레이션 할 수 있지만 시뮬레이션 결과는 시간 관찰과의 정량 비교가 부족합니다. 인터페이스 두께는 일반적으로 실제 상황보다 크게 설정됩니다. 세부 정보가 부족합니다. 네덜란드 델프트 공과 대학의 Marnix Wagemaker (대응 저자)는 Adv.Funct.Mater 저널에 기사를 게재했습니다. 2018 년에는 DFT 데이터를 통합하여 spinel Li4Ti5O12에 리튬 이온을 삽입하기위한 열역학적 위상 필드 모델을 제안합니다. 상 분리 입자의 완전한 열역학적 거동을 설명하는 능력은 최고의 성능의 Li4Ti5O12 전극을 설계하기위한 특정 방향을 제공합니다.
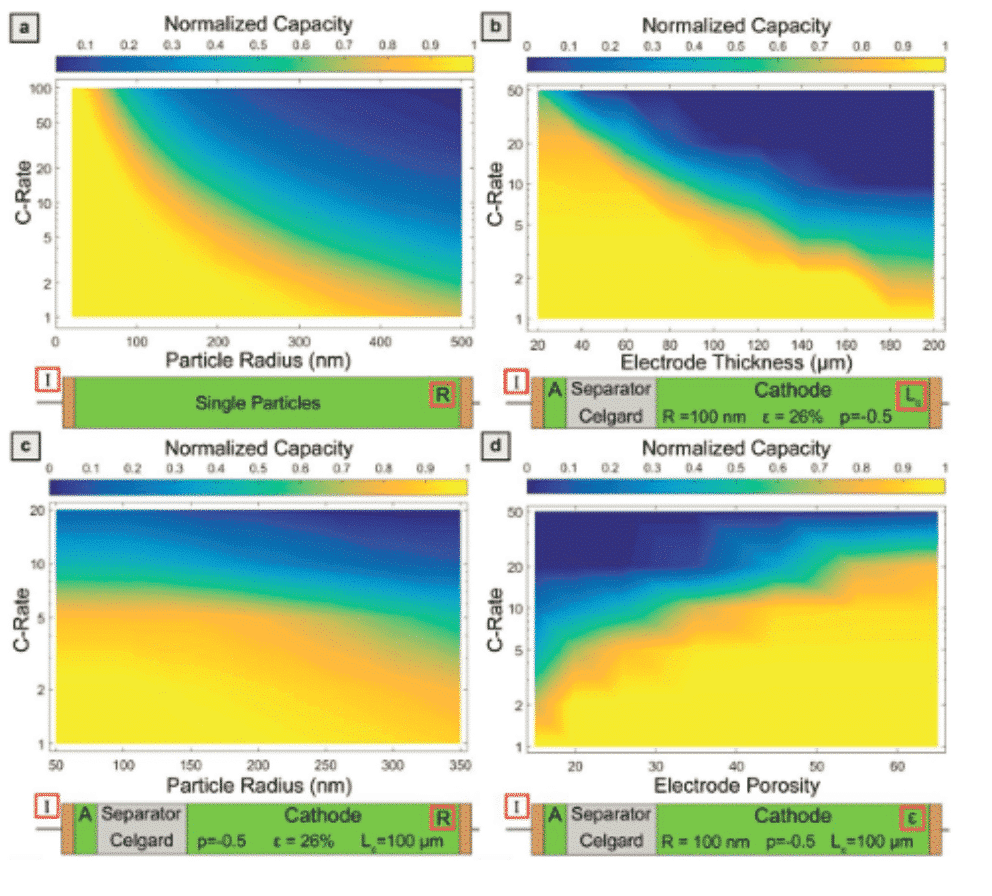
그림 3 : 다공성 전극 시뮬레이션에서 LTO 단일 입자 시뮬레이션, 배터리 용량과 공칭 방전 용량과 전극 두께의 관계
유한 요소 방법
유한 요소법은 편미분 방정식의 경계 값 문제에 대한 근사해를 풀기위한 수치 기법입니다. 유한 요소 방법 시뮬레이션의 흐름은 다음과 같습니다. 1. 솔루션 문제 영역의 이산 2. 영역의 상태 변수 및 변수 제어 방법, 즉 가변 시간 공간의 진화 방정식을 결정합니다. 3. 단일 단위를 도출하고, 단위를 조립합니다. 전체 솔루션이 해결되고, 최종적으로 동시 방정식이 해결되고 결과가 얻어집니다.
전기 자동차용 대용량 및 고출력 리튬 이온 배터리의 과열 거동을 더 잘 이해하기 위해 Xi'an Jiaotong 대학의 Cao Binggang은 유한 요소 방법을 사용하여 내부 저항을 고려하는 동안 배터리의 내부 온도를 시뮬레이션했습니다. 대류 및 외부 소산. 공간 분포, 155°C 고온로에서 테스트 셀의 온도 분포 시뮬레이션 결과 및 VLP50/62/100S-Fe(3.2V/55A·h) LiFePO4/흑연의 배터리 구성.
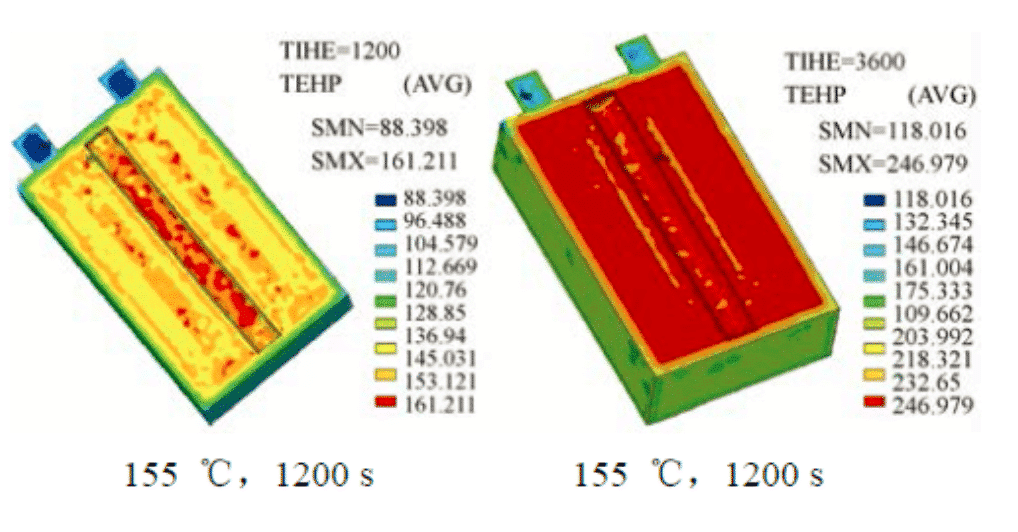
그림 4 : 155 ° C, 1200 초 및 3600 초의 셀에서 유한 요소 시뮬레이션 분포
위상 필드 모델 및 유한 요소 방법과 같은 거시적 재료 시뮬레이션은 엔지니어링 문제에 중점을두고 리튬 이온 배터리의 응력, 열 전달, 흐름 및 다중 필드 커플 링과 같은 거시적 현상을 이해하는 데 도움이됩니다. 밀도 기능 이론에 기초한 1 차 원리 계산은 재료 시스템의 에너지 및 전자 구조와 같은 미세 물리학 적 특성에 더 도움이됩니다.
이론의 개발과 컴퓨터 시뮬레이션의 광범위한 응용으로 컴퓨터 재료 과학은 실험 재료 과학을 이끌고 검증 할 것입니다. 거시적 규모에서 미세한 이론까지의 계산은 리튬 이온 배터리의 재료 분야의 발전을 크게 촉진 할 것입니다. 계산 과학의 도움으로 실험 과학의 많은 문제와 관련하여 명확한 이론적 설명이 될 것입니다. 리튬 이온 배터리의 계산 시뮬레이션 방법에 대한 이해는 리튬 이온 배터리 재료의 개발 및 적용을 가속화 할 것입니다.
참고:
Huang Jie, Ling Shigang, Wang Xuelong 등. 리튬 이온 배터리 (XIV)의 기본 과학 문제 —— 계산 방법 [J]. 에너지 저장 과학 및 기술, 2015, 4 (2) : 215-230.
[2] Ji Xiang, Song Yicheng, Zhang Jungan. 리튬 이온 배터리에서 Li_xC_6의 확산 특성에 대한 분자 역학 시뮬레이션 [J]. 상하이 대학교 저널 (자연 과학), 2014 (1) : 68-74.
[3] Shi Siqi (시시 치). 리튬-이온 배터리 용 양극 재료의 1 차 연구 [D]. 베이징 : 물리 연구소 중국 과학 아카데미, 2004. [4] YangJJ, LiFePO4의 J.S. Li 이온 확산 메커니즘 : abinitio 분자 역학 연구 [J]. J. Phys. 화학 A , 2011,115 (45) : 13045-13049.
Vasileiadis A, Klerk NJJD, Smith RB 등. 위 상장 모델링 [J]을 통해 Spinel Li4Ti5O12 전극의 최적 성능 및 심도있는 이해를 향하여. 고급 기능성 재료, 2018.
Herzmann C, Günther G, Eker B 등 열 남용 응용 분야에서 리튬 이온 배터리의 3 차원 열 유한 요소 모델링 [J]. 전원 저널, 2010, 195 (8) : 2393-2398.








