W ostatnich dziesięcioleciach akumulatory litowo-jonowe przyciągnęły uwagę w dziedzinie materiałów energetycznych. Jednocześnie, wraz z rozwojem podstawowej teorii i pola komputerowego, w badaniach akumulatorów litowo-jonowych zastosowano wiele metod obliczeniowych. Ze względu na błędy w procesie eksperymentalnym, skale mikroskopowe, takie jak mechanizm wzrostu błon SEI, dynamika dyfuzji jonów w materiałach elektrod, ewolucja struktur podczas ładowania i rozładowywania materiałów elektrod, związek między potencjałem a strukturą oraz rozkład warstw ładunku kosmicznego nie może być rozwiązany. Intuicyjne wnioski, metody eksperymentalne nie mogą dać jasnego wyjaśnienia teoretycznego. Natomiast metody symulacji obliczeniowej mają względne zalety w zrozumieniu ewolucji chemii wewnętrznej i elektrochemii akumulatorów litowo-jonowych. Obliczenia teoretyczne weryfikują wyniki eksperymentalne materiałów akumulatorów litowo-jonowych, a także promują i kierują rozwojem materiałów akumulatorowych. Poniżej przedstawiamy kilka powszechnie stosowanych analogowych metod obliczeniowych i ich zastosowania w akumulatorach litowo-jonowych.
Zastosowanie teorii funkcjonalnej gęstości
Teoria funkcjonalna gęstości jest szeroko stosowana w badaniach akumulatorów litowo-jonowych. Jest powszechnie stosowany do obliczania stabilności strukturalnej, potencjału wstawiania litu, struktury elektronicznej, pasma energii, struktury relaksacyjnej, energii generowania defektów, ścieżki migracji, energii aktywacji i litu. Właściwości takie jak kinetyka transportu jonów i deinterkalacja przejść faz litowych.
Wartość napięcia akumulatora jest parametrem związanym ze zmianą swobodnej energii reakcji akumulatora. Różne materiały mają nieodłączny potencjał wstawiania litu. Materiał elektrody idealnie ma wyższy potencjał dla elektrody dodatniej, niższy potencjał dla elektrody ujemnej i różnicę potencjałów między różnymi elektrodami. Moc baterii litowo-jonowej można obliczyć na podstawie reakcji baterii: (1 molowa moc elektronu jest wyrażona przez F, a elektronowa moc jest
1,602 × 10−19 ° C) F = NA · e = = 96487,56 C / mol
Niech n będzie liczbą ładunków przenoszonych podczas reakcji akumulatora, wtedy akumulator przez akumulator wynosi nF, maksymalna praca elektryczna wykonana przez akumulator wynosi:
−Wr’=nFVAVE
W izotermicznych warunkach izostatycznych energia swobodna Gibbsa w systemie jest równa pracy wykonanej przez system na zewnątrz:
ΔG=−Wr’
GG = nFVAVE, a ponieważ Li + ma jednostkę ładunku, VAVE = GG / F
ΔG jest energią swobodną Gibbsa reakcji baterii, przy założeniu, że zmiana objętości i entropii spowodowana reakcją osadzania ogniwa jest znikoma, wówczas
ΔG≈ΔE
więc : VAVE = ΔE / F
W przypadku systemu akumulatorów, w którym elektrodą dodatnią jest LiA, a elektrodą ujemną B, przyjmuje się, że x lit jest usuwany z LiA i osadzony w B po naładowaniu (proces ładowania dodatniego), a wzór reakcji jest następujący:
LiA + B → Li1 − xA + LixB
Średnie napięcie tego procesu stanowi różnicę między energią każdego stanu końcowego odpowiadającego litowi (Li1-xA, LixB) a stanem początkowym (LiA, B), a następnie napięcie:
V = [E (Li1 − xA) + E (LixB) (E (LiA) −E (B)] / xe
Gdy elektrodą ujemną jest lit metaliczny, można to uprościć:
V = [E (Li1 − xA) + E (Lix) −E (LiA)] / xe
Obliczając całkowitą energię każdej substancji przed i po reakcji, potencjał elektrody można obliczyć zgodnie z powyższym wzorem. Jednak dla prawie wszystkich materiałów katodowych napięcie obliczone na podstawie teorii funkcjonalnej gęstości jest niskie. Stosując korektę + U do standardowego GGA, czyli metody GGA + U, lub stosując hybrydową funkcjonalną HSE06, można uzyskać napięcie zbliżone do wartości eksperymentalnej. W obliczeniach materiałów katod tlenkowych zawierających 3d jony metali przejściowych silny efekt korelacji został uznany za efekt, który należy wziąć pod uwagę.
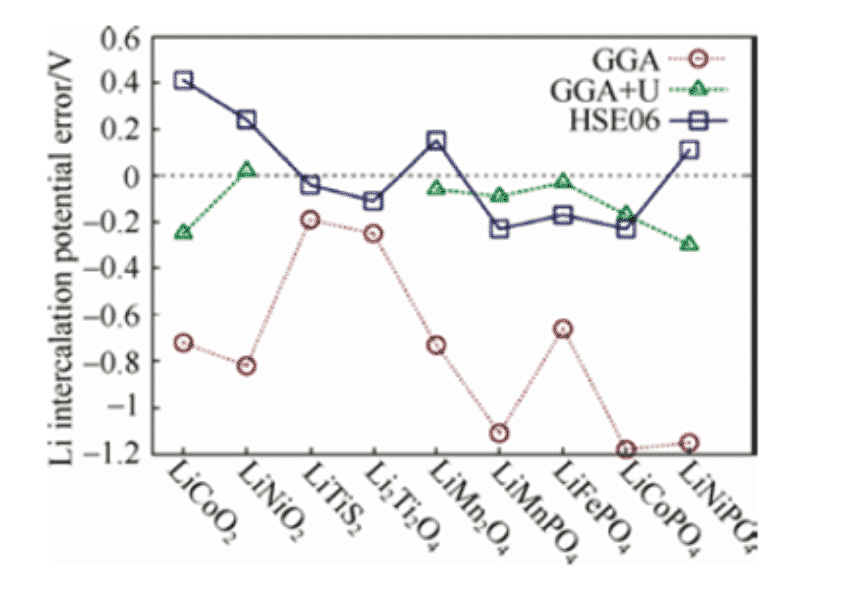
Ryc. 1: Standardowe GGA i GGA + U, HSE06 Oblicz różne jony litu
Metoda dynamiki molekularnej
Pierwotne zasady obliczania oparte na funkcji gęstości mogą uzyskać właściwości materiału w stanie zerowym temperatury gruntu. Transport atomów i jonów w materiale można badać poprzez symulację dynamiki molekularnej w skończonej temperaturze. Obliczenia dynamiki molekularnej stosuje się jako metodę symulacji na poziomie atomowym z wykorzystaniem funkcji potencjału empirycznego. W porównaniu z metodą pierwszorzędną może przeprowadzić symulację na większą skalę, która może lepiej wyświetlać proces dynamicznej dyfuzji jonów litu i analizować go.
Dynamika molekularna może symulować ewolucję cząstek układu w czasie, patrzeć na ścieżkę migracji jonów, obliczać współczynnik dyfuzji cząstek i stabilność materiałów, ale prawem ruchu cząstek jest mechanika newtonowska i istnienie cząstek niskiej jakości takich jak wodór i hel Efekt obliczania efektu kwantowego nie jest idealny. W odniesieniu do akumulatorów litowo-jonowych dynamika molekularna może uzyskać współczynnik dyfuzji i ścieżkę migracji jonów w materiałach, co daje nam możliwość zrozumienia mechanizmu dyfuzji jonów w materiałach.
Yang obliczył proces autodyfuzji LiFePO4 i stwierdził, że migracja Li + w materiale nie zachodzi w sposób ciągły, ale następuje poprzez przejście między sąsiednimi pozycjami sieci. W 2014 roku Zhang Jungan i inni z Uniwersytetu w Szanghaju wykorzystali dynamikę molekularną do symulacji zachowania dyfuzyjnego jonów litu między warstwami grafitu podczas ładowania. Badano właściwości dyfuzyjne jonu litowego materiałów anod grafitowych w temperaturze 300 K. Wyniki eksperymentów dostarczają podstawowych danych do ciągłego badania modelowego deformacji elektrody akumulatora litowo-jonowego.
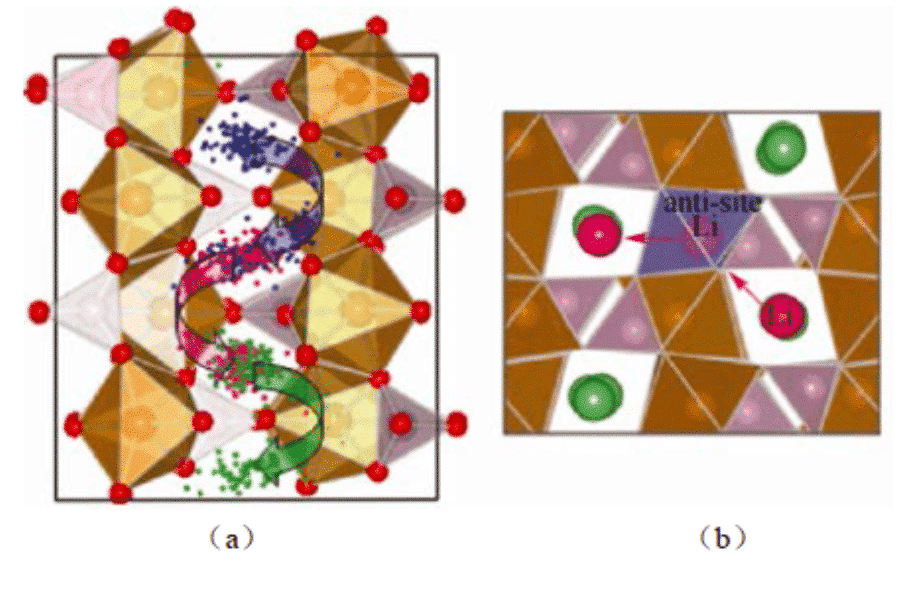
Ryc. 2: Symulacja dynamiki molekularnej pokazuje (a) trajektorię jonów Li w LiFePO4; (b) migracja jonów Li między kanałami poprzez wady wzajemnego zajęcia Li / Fe
Model pola fazowego
Metoda pola fazowego oparta jest na teorii Ginzburga-Landaua. Równanie różniczkowe służy do przedstawienia dyfuzji, potencjału uporządkowania i napędu termodynamicznego określonego mechanizmu fizycznego. Powyższe równania rozwiązuje się za pomocą programowania komputerowego. Zbadaj chwilowy stan systemu w czasie i przestrzeni. Model pola fazowego oparty jest na podstawowych zasadach termodynamiki i dynamiki i jest potężnym narzędziem do przewidywania ewolucji mikrostruktur podczas przejść fazowych w ciele stałym.
Model pola fazowego może symulować wzrost kryształów, transformację fazy stałej, ewolucję pęknięć, przejście fazy filmu, migrację jonów na interfejsie itp., Ale wyniki symulacji to brak porównania ilościowego z obserwacją czasu. Grubość interfejsu jest zwykle ustawiona na większą niż rzeczywista sytuacja. , co prowadzi do braku szczegółów. Marnix Wagemaker (autor korespondent) z Delft University of Technology w Holandii opublikował artykuł w czasopiśmie Adv.Funct.Mater. w 2018 r. zaproponuje termodynamiczny model pola fazowego do wprowadzania jonu litu do spinelu Li4Ti5O12, integrujący dane DFT. Zdolność do opisania pełnego zachowania termodynamicznego cząstek rozdzielonych fazowo zapewnia określony kierunek projektowania najlepszej elektrody Li4Ti5O12.
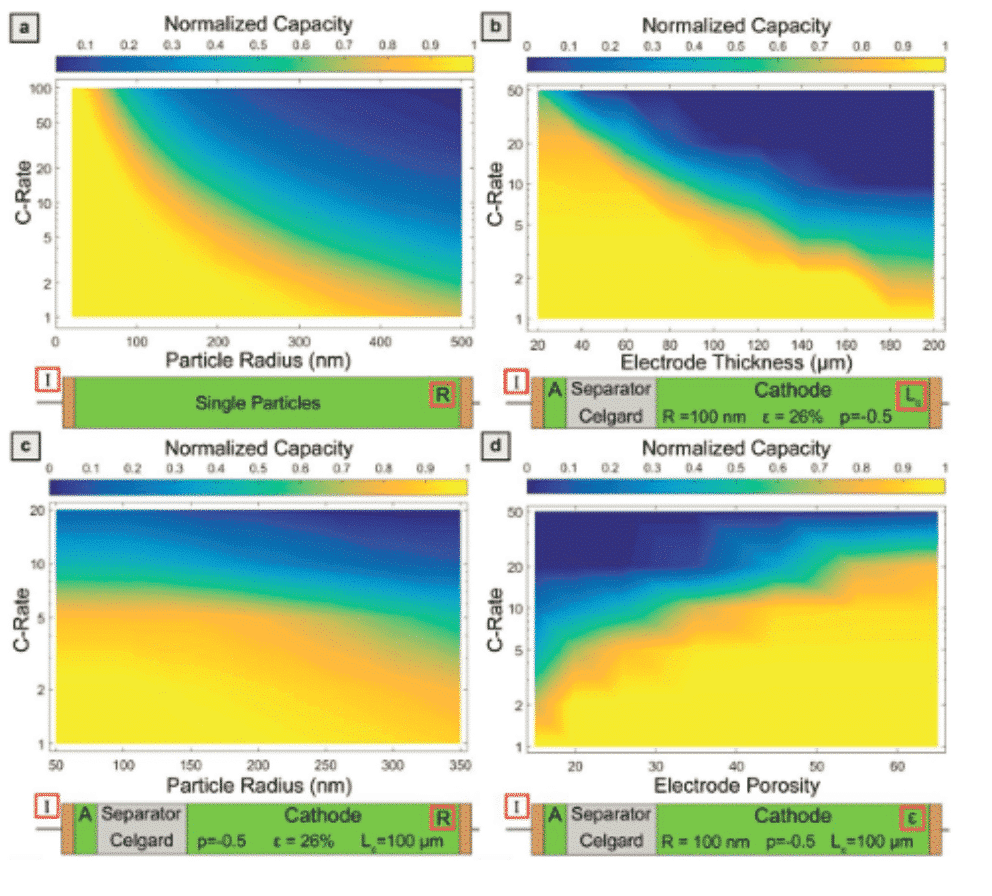
Rysunek 3: Symulacja pojedynczych cząstek LTO, związek między pojemnością baterii a nominalną pojemnością rozładowania i grubością elektrody w symulacji elektrody porowatej
Metoda elementów skończonych
Metoda elementów skończonych jest techniką numeryczną służącą do rozwiązania przybliżonego rozwiązania problemu wartości brzegowych równań różniczkowych cząstkowych. Przebieg symulacji metodą elementów skończonych jest następujący: 1. Dyskretyzacja obszaru problemu rozwiązania 2. Wyznacz zmienną stanu i metodę sterowania zmienną regionu, to znaczy równanie ewolucji zmiennej przestrzeni czasowej; 3. Wyprowadź pojedynczą jednostkę, złóż jednostkę. Ogólne rozwiązanie jest rozwiązane, a na koniec rozwiązane są równania równoczesne i uzyskane wyniki.
In order to better understand the overheating behavior of large-capacity and high-power lithium-ion batteries for electric vehicles, Cao Binggang of Xi’an Jiaotong University used finite element method to simulate the internal temperature of the battery during consideration of internal resistance, convection and external dissipation. The spatial distribution, the temperature distribution simulation results of the test cell in a 155 °C hot furnace and the battery composition of VLP50/62/100S-Fe (3.2 V/55 A·h) LiFePO4/graphite.
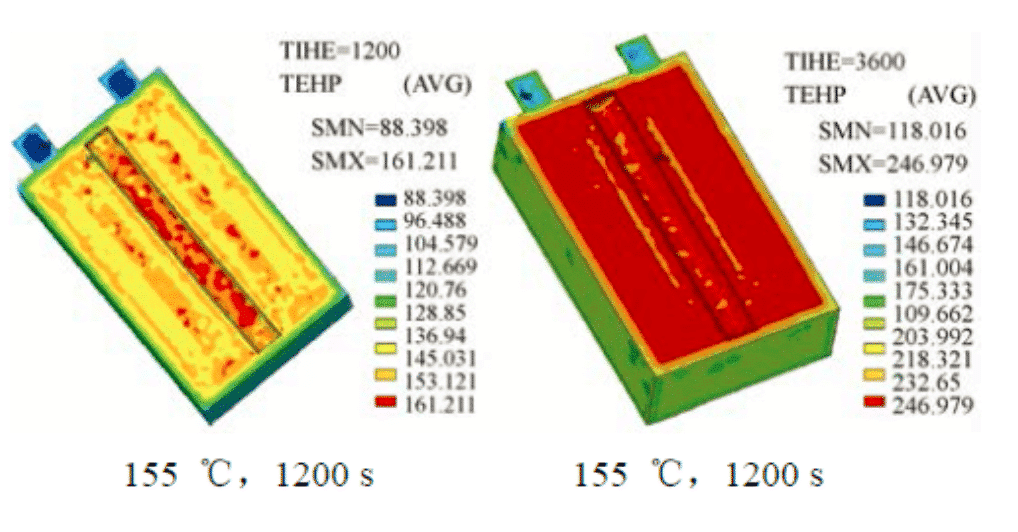
Rycina 4: Rozkład symulacji elementów skończonych w komórce w 155 ° C, 1200 si 3600 s
Symulacje makroskopowe materiałów, takie jak modele pola fazowego i metody elementów skończonych, koncentrują się na zagadnieniach inżynierskich i pomagają zrozumieć zjawiska makroskopowe, takie jak naprężenia, przenoszenie ciepła, przepływ i sprzężenie wielopolowe w akumulatorach litowo-jonowych. Pierwotne zasady obliczania oparte na teorii funkcjonalnej gęstości bardziej sprzyjają właściwościom fizykochemicznym, takim jak energia i struktura elektronowa układu materiałowego.
Wraz z rozwojem teorii i szerokim zastosowaniem symulacji komputerowych nauka o materiałach obliczeniowych poprowadzi i zweryfikuje naukę o materiałach eksperymentalnych. Obliczenia od skali makroskopowej po teorię mikroskopową znacznie przyczynią się do rozwoju pola materiałowego dla akumulatorów litowo-jonowych. Pod względem wielu problemów w nauce eksperymentalnej, przy pomocy symulacji obliczeniowych, będzie to również jasne wyjaśnienie teoretyczne. Zrozumienie metod obliczeniowych symulacji akumulatorów litowo-jonowych przyspieszy rozwój i zastosowanie materiałów akumulatorów litowo-jonowych.
Odniesienie:
[1] Huang Jie, Ling Shigang, Wang Xuelong i in. Podstawowy problem naukowy dotyczący baterii litowo-jonowej (XIV) —— Metoda obliczeniowa [J]. Energy Storage Science and Technology, 2015, 4 (2): 215–230.
[2] Ji Xiang, Song Yicheng, Zhang Jungan. Symulacja dynamiki molekularnej właściwości dyfuzyjnych Li_xC_6 w bateriach litowo-jonowych [J]. Journal of Shanghai University (Natural Science), 2014 (1): 68-74.
[3] Shi Siqi (Sisi Qi). Badanie podstawowych zasad materiałów katodowych do akumulatorów litowo-jonowych [D]. Beijing: Institute of Physics Chinese Academy of Sciences, 2004. [4] Yang JJ, Tse J S. Mechanizmy dyfuzji jonów Li w LiFePO4 study Badanie dynamiki molekularnej abinitio [J]. J. Phys. Chem. A, 2011, 115 (45) : 13045-13049.
[5] Vasileiadis A, Klerk NJJD, Smith RB i in. W kierunku optymalnej wydajności i dogłębnego zrozumienia elektrod Spinel Li4Ti5O12 za pomocą modelowania fazowego [J]. Zaawansowane materiały funkcjonalne, 2018.
[6] Herzmann C, Günther G, Eker B, i in. Trójwymiarowe modelowanie termiczne elementów skończonych baterii litowo-jonowych w zastosowaniach nadużywania ciepła [J]. Journal of Power Sources, 2010, 195 (8): 2393–2398.








