密度汎関数理論(DFT)は、多粒子システムを扱うための近似法として、凝縮物質物理学、材料科学、量子化学、生命科学の分野で広く使用されています。たとえば、図1(c)は、DFT法を使用して計算された72原子のスーパーセル構造です[1]。 DFTベースの材料科学計算シミュレーション手法は、既存の材料を研究できるだけでなく、新しい材料を予測することもできます。
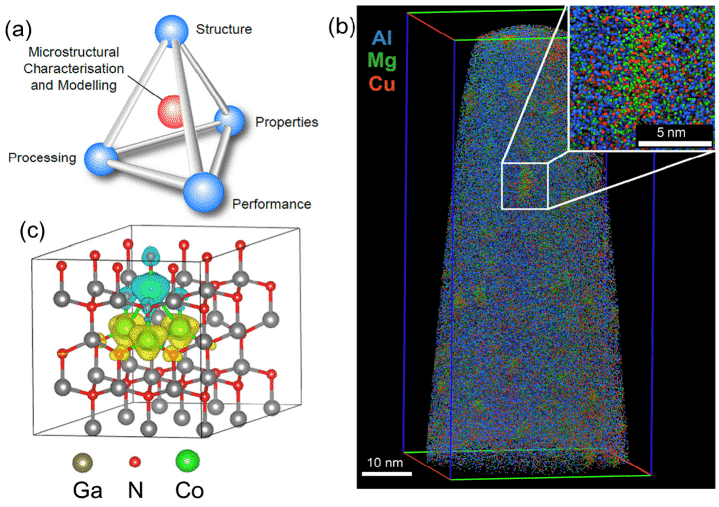
図1(a)微視的特性評価、構造、処理、特性および特性間の潜在的なリンク、(b)約2000万個の原子を含むAl-Cu-Mg合金のAPTデータ、(c)DFT計算用の72原子スーパーセルの例
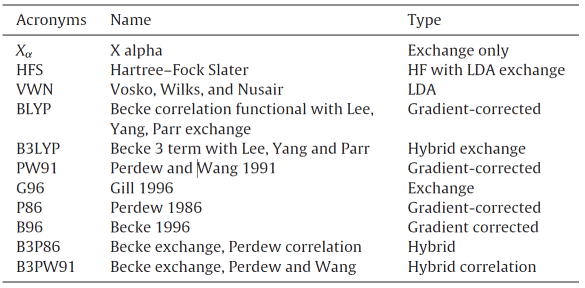
関数は、ベクトル空間から関数の関数であるスカラーへのマッピングです。表1に、提案されている密度汎関数のタイプのいくつかをリストします。これらのいくつかは、基本的な量子力学から派生したものと、パラメトリック関数から派生したもので、それぞれ独自の長所と短所、および適用範囲があります[2]。 DFT法の本質は、単一電子の波動関数ではなく、分子(原子)基底状態のすべての情報のキャリアとして電子密度を使用することです。これにより、マルチ電子システムを単一電子問題。電子の数をNとすると、波動関数の変数の数は3Nであり、密度汎関数理論は変数の数を3つの空間変数に減らします。これにより、計算プロセスが簡略化され、計算精度が保証されます。
表1いくつかの近似密度汎関数タイプ
密度汎関数理論の開発は、大きく3つの段階に分けることができます。最初の段階は1927年でした。トーマスとフェルミは、理想的な条件下での理想的な電子ガス仮説に基づいてトーマス-フェルミモデルを提案しました。初めて密度汎関数理論の概念が導入され、後のDFT法のプロトタイプとなりました。
Thomas-Fermiモデルの開始点は、電子間に相互作用がなく、外部干渉がないと仮定することです。その場合、電子運動のシュレーディンガー方程式は次のように表すことができます。
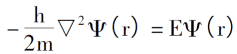
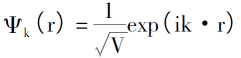
0Kでの電子配置の法則を導入すると、電子密度、単一電子の全エネルギー、およびシステムの運動エネルギー密度は次のようになります。
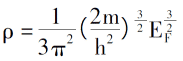
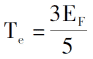
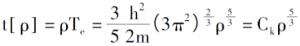
電子間のクーロンポテンシャルと外部場の説明を導入することにより、電子密度関数のみによって決定される電子システムの総エネルギー表現を導出できます[3]。
モデルは計算のフォームとプロセスを簡略化しますが、電子間の相互作用は考慮していません。運動エネルギーの項目を正確に説明していないため、多くのシステムには適用できません。しかし、この新しい研究のアイデアに触発されて、関連する学者たちは基本的に長年の努力の後で1960年代に密度汎関数理論の内容を完成させ、最終的に厳密な密度汎関数理論を確立しました。
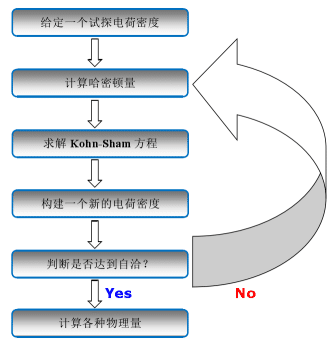
図2 DFTに基づく自己矛盾のない反復プロセスの概略図
Hohenberg-Kohnの定理とKohn-Shamの方程式は、DFT法の形成と改善に重要な役割を果たしており、DFTの2つの礎石として歓迎されています。
(1)ホーエンベルク=コーンの定理
Hohenberg-Kohnの定理の核となる考え方は、システム内のすべての物理量は電子密度のみを含む変数によって一意に決定できることであり、実装方法は、変分原理によってシステムの基底状態を取得することです。この理論は、主に不均一な電子ガスモデル用であり、2つのサブ定理で構成されています。 i)外部ポテンシャル(電子相互作用以外のポテンシャル)のスピンを無視する電子システム。外部ポテンシャルは電子密度によって一意に決定できます。 ii)与えられた外部ポテンシャルに対して、システムの基底状態エネルギーはエネルギー関数値の最小値です。したがって、システムのエネルギー汎関数は次のように説明できます。
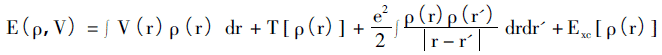
方程式の右側は、ポテンシャルエネルギー、運動エネルギーの項、電子間のクーロン相互作用、および外部フィールドの交換に関連するポテンシャルエネルギーです。
この定理は、電子密度関数、運動エネルギー汎関数、および交換関連の汎関数の特定の表現を与えないため、特定の解はまだ不可能です。
(2)コーンシャム方程式
1965年まで、KohnとShen Lujiuは、Kohn-Sham方程式を確立して、各項目の詳細を説明し、密度汎関数理論が実用化段階に入り始めました。彼らは、運動エネルギー汎関数が相互作用なしで粒子運動エネルギー汎関数を使用して置換を近似することを提案し、2つの間の差は交換関連汎関数の未知数に含まれています[4]。ρの変動は、 Φi(r)の変化であり、ラグランジュ乗数はEiに置き換えられます。単一電子方程式は次のとおりです。
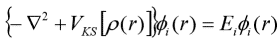
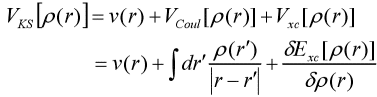
上記はKohn-Sham方程式です。
コーン・シャム方程式は、交換に関連する関数以外のすべてに明確な表現を与え、複雑な効果をこの用語に分類します。この時点で、計算の難しさが大幅に簡略化され、すべての作業は交換関連の機能拡張を記述する方法を中心に始まります。同時に、交換に関連するポテンシャルのおおよその形式も、密度汎関数理論の精度を直接決定します。
Local Density Approximation(LDA)法は、1965年にKohnとShen Lujiuによっても提案されました。目的は、未知の交換結合を近似し、DFT法を実際の計算に使用できるようにすることです。 LDAは、均一な電子ガスの密度関数を使用して、不均一な電子ガスの交換関係を計算します。システム内の電子密度が空間によってほとんど変化しないと仮定すると、不均一な電子ガスの交換関係は次のように表すことができます。
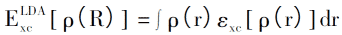
対応する交換相関ポテンシャルは、次のように表すことができます。
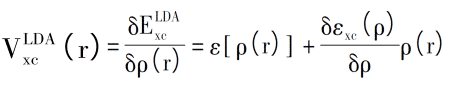
たとえば、Asad Mahmood et al。はVASPを使用して、LDA-PBEおよびGGA-PAW計算の平衡構造パラメーターを比較し、電子軌道ハイブリダイゼーションに対するGaドーピングの影響、ならびに光学特性と結晶形状を図3(c)から研究しました。 Ga-2sおよびGa-2p軌道が伝導に大きく寄与し、VBが低いのもGa-2pによるものであり、CBの下部の不純物バンドが追加のエネルギー障壁であるVB間の電子を示唆していることがわかりますとCB。遷移はエネルギー障壁を超えなければなりません[5]。
図3計算結果
(a)最適化された3x3x3 GaドープZnOスーパーセル、(b)バンド構造、(c)密度DOS
実際の材料システムをより正確に計算するために、1986年にBecke、Perdew、Wangなど。提案された一般化勾配近似(GGA)は、密度汎関数計算で最も広く使用されている処理方法です。
GGA処理方法は、元の表現を電子密度関数と勾配関数、およびスピンの説明を含む関数形式に書き換えることであり、結果として生じる交換関連の関数は次のようになります。
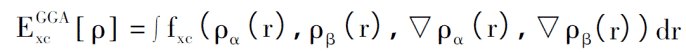
GGAでは、交換相関ポテンシャルも交換エネルギーと相関エネルギーに分解できます。では、これら 2 つの部分を適切に表現するにはどうすればよいでしょうか。 Beckc等。 GGA-PW91 のように、具体的な機能形式は原則として任意に構成でき、実際の物理的意味を考慮する必要はないと考えています。 Perdew等の間。可能な限り純粋な量子力学計算理論に戻ることを提唱し、すべての物理量は計算のみです。関数式は、電子の静質量、プランク定数、光速などの基本的な定数から始まり、凝縮系などの分野でよく使われる GGA-PBE (Perdew-Burke-Enzerhoff) などの経験的パラメータを過度に含んではいけません。物理。
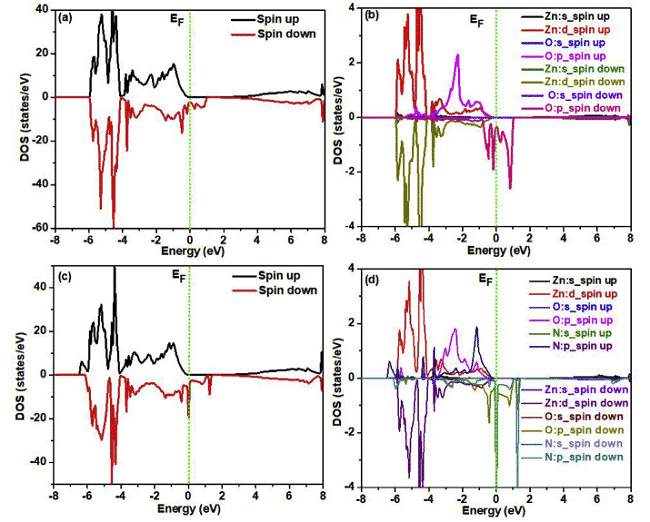
最近、Parmod KumarとL. Romakaら。 WIEN2kおよびElk v2.3.22でそれぞれFP-LAPW(完全ポテンシャル線形強化平面波)を使用して関連する研究を実施しました。ここで、交換相関ポテンシャルはGGA-PBEの形式であり、図4、5対応する計算結果状態密度と電荷密度分布[6,7]。
図4 N注入および注入なしのスピン分極ZnOスーパーセルの総状態密度および局所状態密度
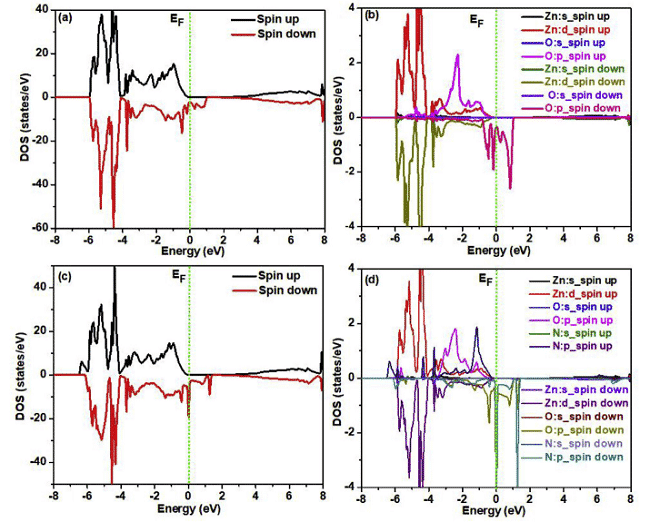
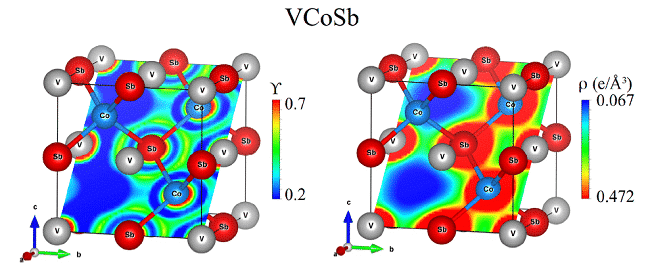
図5 VCoSbテルル化物における電子局在関数(Y)と電荷密度(r)の分布J.Ibáñez、T。Woźniaket al。圧力下のHfS2の格子力学を予測するために、異なる密度汎関数理論の有効性をテストしました。
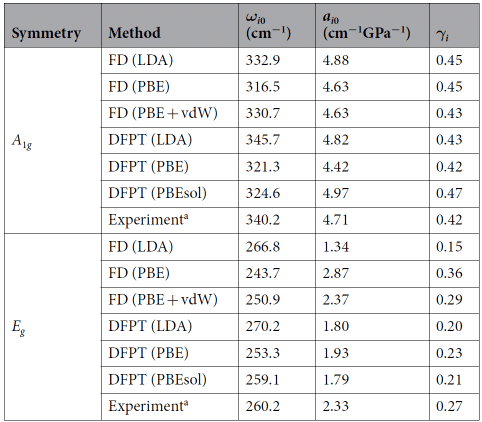
観察表2では、GGA-DFTがvdW相互作用を考慮したHfS2の高圧格子ダイナミクスを適切に記述しているのに対し、LDA-DFT計算は環境条件下での2D化合物の構造と振動特性を予測するために広く使用されており、圧縮下では再現できないことがわかりました条件。 HfS2の動作は、DFT-LDAを使用してTMDCとグリューナイゼンパラメーターの圧縮率を計算すると、大きなエラーが発生することを示しています[8]。
表2ラマン周波数(ωi0)、圧力係数(ai0)、グリューナイゼンパラメーター(γi)
LDAおよびGGAアルゴリズムに加えて、Hatree-Fock(HF)交換効果をハイブリッド方式で交換アソシエーションに組み込むハイブリッド密度汎関数もあります。たとえば、B3LYPは1998年に人気がありました。これらの理論には、体系的な情報と計算結果は、特に有機化学の分野に適した実験データにますます近づいており、化学反応機構の計算において大きな成功を収めています。
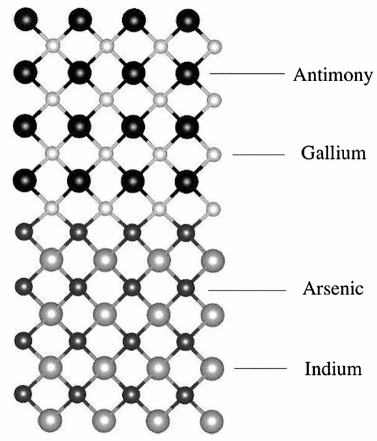
例えば、T。Garwood et al。は、実験値に非常に近いPBE0タイプのハイブリダイゼーション[9]を使用して、InAs / GaSb IIタイプの超格子構造(図6に示すモデル)のバンドギャップデータを計算し、偏差範囲は約3 %-11%です。
図6 VESTAを使用して計算されたハイブリッドDFTのボールアンドスティックInAs / GaSb SLSモデル
Kohn-Sham単一粒子エネルギースペクトルに基づく電子バンド構造理論は、多くの材料を定性的に説明できますが、定量的な観点からは満足のいくものではありません。たとえば、SiやGaAsなどの単純な半導体材料の場合、LDA / GGのもとでKohn-Sham DFTによって与えられるバンドギャップははるかに小さくなります。 GeやInNなどの小さなバンドギャップ半導体の場合、LDA / GGAから得られる金属は金属です。状態ですが、実験的観察は半導体であり、これはいわゆるLDA / GGAバンドギャップ問題です。
バンド ギャップの問題を克服するために、人々は DFT の理論的枠組みで多くの努力をしてきました。たとえば、局所有効ポテンシャルに基づくコーン シャム理論を、非ポテンシャルに基づく一般化コーン シャム (GKS) 理論に拡張するなどです。局所有効ポテンシャル、およびその他の混成密度汎関数理論として、1 体グリーン関数に基づく多体摂動理論があります。この理論では、Kohn-Sham DFT による交換関連のポテンシャルは、交換関連の自己エネルギー演算子に対応します。自己エネルギー演算子の場合、比較的単純で正確な近似は GW 近似 (単一粒子のグリーン関数 G とシールドされたクーロン効果 W の積) です。特定の近似の下で自己エネルギー演算子を計算することにより、対応する PES (IPS) を取得できます。励起エネルギー中の準粒子。これらの新しい開発方向により、材料のバンド ギャップの記述が改善されましたが、近似汎関数には依然として大きな主観性があり、適用範囲は比較的限られています。これまでのところ、十分な理論的根拠を備えた普遍的な DFT 法はありません。材料の電子バンド構造の正確な説明 [10,11]。
さらに、既存の密度汎関数理論に基づくいくつかの拡張があります。たとえば、KS軌道エネルギー差に基づく時間依存密度汎関数理論(TDDFT)は、Schordinger方程式を単一粒子のディラック方程式に置き換えるために使用されます。密度密度汎関数理論は、強相関システムのLDA + Uと、任意の磁場の下で相互作用する電子システムを扱うための流れ密度汎関数理論(CDFT)にまで及びます。
参考文献
Xiang-Yuan Cui、Simon P. Ringer、アトムプローブ顕微鏡法と密度汎関数理論シミュレーションの間のつながりについて[J]、材料
特性評価(2018)、https://doi.org/10.1016/ matchar.2018.05.015
B.オボット、DDマクドナルド、ZMガセム、密度汎関数理論
(DFT)新しい有機腐食抑制剤を設計するための強力なツールとして。パート1:概要[J]、Corrosion Science 99(2015)1–30
Geerlings、F。De Proft、W。Langenaeker、概念密度汎関数理論、Chem。 Rev. 103(2003)1793–1873。
Nagy、密度汎関数理論および原子と分子への応用、Rev.298(1998)1–79。
Koch、MC Holthausen、密度汎関数理論への化学者ガイド、Wiley-VCH、Weinheim、2000年。
Asad Mahmood、Fatih Tezcan、Gulfeza Kardas、ゾルゲル由来のZn0.8Ga0.2O前駆体ゲルの熱分解:無速度論的、熱力学的、およびDFTの研究[J]、Acta Materialia 146(2018)152-159
パルモドクマール、ヒテンドラK.マリク、アニマゴーシュ、R。タンガヴェル、K。アソカン、ZnOとNの強磁性の起源への洞察
注入されたZnO薄膜:実験およびDFTアプローチ[J]、合金と化合物のジャーナル768(2018)323-328
Romaka、VV Romaka、N。Melnychenko、Yu。 Stadnyk、L。Bohun、A。Horyn、VeCoeSb 3成分系の実験およびDFT研究[J]、合金と化合物のジャーナル739(2018)771-779
Ibáñez、T。Woźniak、F。Dybala、R。Oliva、S。Hernández、R。 Kudrawiec、バルクHfS2における高圧ラマン散乱:層状MS2化合物(M = Hf、Mo)における密度汎関数理論法の圧縮下での比較[J]、科学報告書(2018)8:12757、DOI:10.1038 / s41598-018- 31051-y
ガーウッド、NAモディーン、S。クリシュナ、ハイブリッド密度汎関数理論によるInAs / GaSb超格子の電子構造モデリング[J]、Infrared Physics&Technology 81(2017)27–31
ユージーン・S・クリャチコ、エドゥアルド・V・ルデナ、密度汎関数理論:レビューされた基礎[J]、Physics Reports 544(2014)123–239
B.オボット、DDマクドナルド、ZM Gasem、密度汎関数理論(DFT)は、新しい有機腐食防止剤を設計するための強力なツールです。パート1:概要[J]、Corrosion Science 99(2015)1–30








